SCIENZE E TECNOLOGIE INFORMATICHE

Fino ad ora si è sempre partiti da una retta per rappresentarla sul piano, ma se deve invece partire da due punti per trovare l’equazione della retta come si fa?

Allora il concetto che un punto appartiene alla retta significa che sostituisco i valori di x e di y nell’equaione di partenza, ho l’identità.

Ad esempio se devo trovare la retta passante per i punti A(1;0) e B(0;1) si parta da y = mx + q e mi troverò un sistema di equazioni di primo grado con incognite m e q.

0 = m*1 + q

1 = 0*m +q ossia q = 1 ed m utilizzando il metodo della sostituzione diventerà:

m = -1.

La retta passante per A (1;0) e B(0;1) sarà:

y = -x + 1

[:it]

Claudio Souza Pinto

Rappresentare sul piano cartesiano le seguenti rette.

Esercizi per un livello sufficiente [6] :

6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.

Esercizi per un livello discreto [7] :

7.1.
7.2.
7.3.
7.4.
7.5.
7.6.
7.7.
7.8.
7.9.
7.10.

Esercizi per un livello buono [8] :

8.1.

8.2.

8.3.

8.4.

8.5.

8.6.

[:en]Rappresentare sul piano cartesiano le seguenti rette:

1) y= 3x + 5

2) y=-2x-1

3) y=1/3x-3

4) y=-x-4

5) 6x-5y+8=0

6) 2x – 6y-1 =0

7) x+y-10 = 0

8)x-y=0

9) 4x – 5 = 0

10) 3y – 5 = 0

11) 2y-7x = 0

12) 4x = 0[:de]Rappresentare sul piano cartesiano le seguenti rette:

1) y= 3x + 5

2) y=-2x-1

3) y=1/3x-3

4) y=-x-4

5) 6x-5y+8=0

6) 2x – 6y-1 =0

7) x+y-10 = 0

8)x-y=0

9) 4x – 5 = 0

10) 3y – 5 = 0

11) 2y-7x = 0

12) 4x = 0[:]

[:it]

Claudio Souza Pinto

Una delle regole fondamentali sulle rette è la condizione di parallelismo o di perpendicolarià.

Data una retta: 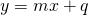ed una retta 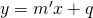, esse sono:

parallele quando m = m’

perpendicolari quando m = – 1/m’

Ad esempio date le rette:

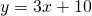e la retta 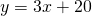esse sono parallele perché il numero che moltiplica la 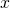è uguale.

Ad esempio date le rette:

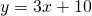e la retta 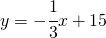sono perpendicolari in quanto il numero che moltiplica la 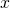sono uno il reciproco e l’opposto dell’altro.

[:en]Quando unisco due punti creo un segmento, se questo viene prolungato ai suoi estremi mi trovo una retta.

Una retta mette in relazione l’asse delle y con l’asse delle x.

In generale una retta viene scritta come:

y = m*x + q

m è il coefficiente angolare

q l’ordinata all’origine

Ad esempio y = 2*x + 3 è una retta mentre y = x^2+ 3x + 9 è un’altra curva che si può anch’essa disegnare sul piano caretesiano ma NON è una retta.

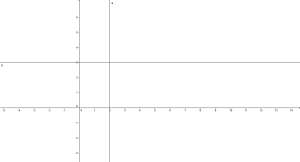
Come faccio a rappresentare una retta sul piano cartesiano?

Fondamentale: sono sufficienti due punti per rappresentare una retta! SOLO DUE ossia è sufficiente prendere un valore a caso di x ed uno di y oppure due di x o due di y, l’altra incognita si trova partendo dall’equazione della retta.

Ad esempio se y= 2*x + 2 prendo il valore x = 0 (zero) troverò che y = 2* 0 + 2=2 ed ho trovato il punto A(0;2). Poi prendo y=0 allora avrò 0 = 2*x + 2 ossia x = -1 per cui il secondo punto è B(-1;0).

Segno i due punti sul piano cartesiano, li unisco ed ho proprio la retta.

 Una delle regole fondamentali sulle rette è la condizione di parallelismo o di perpendicolarità.

Due rette sono parallele quando m = m’

Due rette sono perpendicolari quando m = – 1/m’

[:de]Quando unisco due punti creo un segmento, se questo viene prolungato ai suoi estremi mi trovo una retta.

Una retta mette in relazione l’asse delle y con l’asse delle x.

In generale una retta viene scritta come:

y = m*x + q

m è il coefficiente angolare

q l’ordinata all’origine

Ad esempio y = 2*x + 3 è una retta mentre y = x^2+ 3x + 9 è un’altra curva che si può anch’essa disegnare sul piano caretesiano ma NON è una retta.

Come faccio a rappresentare una retta sul piano cartesiano?

Fondamentale: sono sufficienti due punti per rappresentare una retta! SOLO DUE ossia è sufficiente prendere un valore a caso di x ed uno di y oppure due di x o due di y, l’altra incognita si trova partendo dall’equazione della retta.

Ad esempio se y= 2*x + 2 prendo il valore x = 0 (zero) troverò che y = 2* 0 + 2=2 ed ho trovato il punto A(0;2). Poi prendo y=0 allora avrò 0 = 2*x + 2 ossia x = -1 per cui il secondo punto è B(-1;0).

Segno i due punti sul piano cartesiano, li unisco ed ho proprio la retta.

 Una delle regole fondamentali sulle rette è la condizione di parallelismo o di perpendicolarità.

Due rette sono parallele quando m = m’

Due rette sono perpendicolari quando m = – 1/m’

[:]

[:it]

Renè Magritte

Un esercizio classico sul piano cartesiano è identificare la distanza tra due punti.

Per fare questo è sufficiente applicare sempre la seguente formula:

con e

La cosa importante è mantenere sempre la differenza tra le coordinate.

Ad esempio dati i seguenti due punti A(1;0) e B(0;1); bisogna calcolare la distanza tra questi due punti:

 che è circa 1,41.

[:en]

Renè Magritte

Un esercizio classico sul piano cartesiano è identificare la distanza tra due punti.

Per fare questo è sufficiente applicare sempre la seguente formula:

con e

La cosa importante è mantenere sempre la differenza tra le coordinate.

Ad esempio dati i seguenti due punti A(1;0) e B(0;1); bisogna calcolare la distanza tra questi due punti:

 che è circa 1,41.

1) Calcola la distanza tra A(3;4) e B (1;2)

2) Calcola la distanza tra A(5,4) e B(8,4)

3) Calcola la distanza tra A(-2,3) e B(4,3)

4) Calcola la distanza tra A(3,5) e B(-6,-4)

5) Calcola la distanza tra A(-5,0) e B(-8,2)

6) Calcola la distanza tra A(-1/2,-1/2) e B(1,1)

[:de]

Renè Magritte

Un esercizio classico sul piano cartesiano è identificare la distanza tra due punti.

Per fare questo è sufficiente applicare sempre la seguente formula:

con e

La cosa importante è mantenere sempre la differenza tra le coordinate.

Ad esempio dati i seguenti due punti A(1;0) e B(0;1); bisogna calcolare la distanza tra questi due punti:

 che è circa 1,41.

1) Calcola la distanza tra A(3;4) e B (1;2)

2) Calcola la distanza tra A(5,4) e B(8,4)

3) Calcola la distanza tra A(-2,3) e B(4,3)

4) Calcola la distanza tra A(3,5) e B(-6,-4)

5) Calcola la distanza tra A(-5,0) e B(-8,2)

6) Calcola la distanza tra A(-1/2,-1/2) e B(1,1)

[:]

[:it]

File/Rene%20Magritte%20-%20The%20Happy%20Hand%20.JPG” alt=”” width=”277″ height=”214″ data-bm=”71″ /> Renè Magritte

Il piano cartesiano consente di rappresentare visivamente l’andamento di una variabile rispetto ad un’altra.

Ad esempio posso rappresentare sul piano cartesiano l’andamento nel tempo del numero di pasti che vengono preparati ogni giorno all’interno di una mensa. Se questo andamento rappresenta una ciclicità (ripetizione dell’andamento della curva) si possono prevedere le quantità da acquistare ed un eventuale possibilità di ottimizzare le risorse o fare nuovi investimenti.

Il piano cartesiano venne introdotto da Cartesio (matematico francese) nel 1637: egli cercò cos’ di fondere l’algebra con la geometria.

Cogito ergo sum

E’ una delle frasi celebri di Cartesio che mette in evidenza che solo pensando posso dimostrare di distinguermi da altre forme di vita e posso migliorare la mia condizione.

Nomenclatura:

Asse x o asse delle ascisse è quella orizzontale.

Asse y o asse delle ordinate è quella verticale.

Un punto sul piano cartesiano è identificato da due numeri o coordiate la prima è sempre riferita alle x, la seconda alle y e se ce ne fosse una terza alle z.

Un punto quindi si identifica in tale maniera P(2;3) non si mette l’uguale vicino alla P ma direttamente la parentesi e i due numeri divisi o da un punto e virgola o da una virgola soltanto. Si fisssa il numero 2 sulle x e si tira su una riga verticale. Si fissa il 3 sull’asse delle y e si tira una riga oriozzontale: il punto d’incrocio rappresenta il punto

P(2;3)

L’applicazione immediata è nella cartografia che non dimentichiamo ebbe un grandissimo sviluppo proprio nel bacino del mediterraneo e nella nostra penisola famosa per le Repubbliche marinare (Venezia, Genova, Amalfi e Pisa).

[:de]

Renè Magritte

Il piano cartesiano consente di rappresentare visivamente l’andamento di una variabile rispetto ad un’altra.

Ad esempio posso rappresentare sul piano cartesiano l’andamento nel tempo del numero di pasti che vengono preparati ogni giorno all’interno di una mensa. Se questo andamento rappresenta una ciclicità (ripetizione dell’andamento della curva) si possono prevedere le quantità da acquistare ed un eventuale possibilità di ottimizzare le risorse o fare nuovi investimenti.

Il piano cartesiano venne introdotto da Cartesio (matematico francese) nel 1637: egli cercò cos’ di fondere l’algebra con la geometria.

Cogito ergo sum

E’ una delle frasi celebri di Cartesio che mette in evidenza che solo pensando posso dimostrare di distinguermi da altre forme di vita e posso migliorare la mia condizione.

Nomenclatura:

Asse x o asse delle ascisse è quella orizzontale.

Asse y o asse delle ordinate è quella verticale.

Un punto sul piano cartesiano è identificato da due numeri o coordiate la prima è sempre riferita alle x, la seconda alle y e se ce ne fosse una terza alle z.

Un punto quindi si identifica in tale maniera P(2;3) non si mette l’uguale vicino alla P ma direttamente la parentesi e i due numeri divisi o da un punto e virgola o da una virgola soltanto. Si fisssa il numero 2 sulle x e si tira su una riga verticale. Si fissa il 3 sull’asse delle y e si tira una riga oriozzontale: il punto d’incrocio rappresenta il punto

P(2;3)

L’applicazione immediata è nella cartografia che non dimentichiamo ebbe un grandissimo sviluppo proprio nel bacino del mediterraneo e nella nostra penisola famosa per le Repubbliche marinare (Venezia, Genova, Amalfi e Pisa).

[:]

1) Un capitale scade fra tre anni e 7 mesi. Il suo valore attuale, calcolato con sconto commerciale al tasso del 9,5% è di 989,37€. Calcola il capitale.

2) Il capitale di 1080€ scade fra 2 anni e 18 mesi. Il suo valore attuale con sconto commerciale è di €907,31. A quale tasso è stato concesso lo sconto?

3) Il capitale di 975€ scade fra 101 giorni. Il suo valore attuale con sconto comemrciale è di 944,14€. A quale tasso è stato concesso lo sconto?

4) Il capitale di 3320€ scade fra un certo tempo. Il suo valore attuale, calcolato con sconto commerciale al tasso del 9,6% è di €2966,08. Fra quanto tempo scade quel capitale?

5) Una cambiale di €440 viene scontata 20 giorni prima della scadenza. Il valore attuale ricavato è di €425,33. A quale tasso è stato concesso lo sconto semplice?

6) Una cambiale di €1880 viene scontata al tasso del 7,25%. Il valore attuale ricavato è di 1771. Calcola quanto tempo prima della scadenza è stata effettuata l’operazione di sconto semplice.

7) Calcola il valore attuale con sconto composto al 16% del capitale di €800 esigibile fra 8 anni.

8) Calcola il valore attuale con sconto composto al 6% del capitale di €980 esigibile fra 4 anni, 5 mesi e 18 giorni.

9) Calcola il valore attuale con sconto composto al 6,2% del capitale di €1060 esigibile fra 5 mesi  e 18 giorni

10) un capitale scade fra 120 giorni. Il valore attuale calcolato al 9% e con sconto semplice. supera di 900€ quello calcolato con sconto commerciale, sempre allo stesso tasso. Calcola il capitale.

11)Si considerino i seguenti capitali 380€ esigibili fra 1 anno e 5 mesi, 740€ esigibili fra due anni. Determiona il valore attuale complessivo nel caso in cui usando un tasso del 9%:

a) il primo venga scontato con sconto commerciale e il secondo con sconto composto;

b) entrambi vengano scontati con sconto comemrciale;

c) entrambi vengano scontati con sconto composto.

12)Una persona deve incassare la somma di 4444 fra 3 anni e 1 mese. Cede oggi questo diritto rivevendo il valore attuale con sconto commerciale al tasso dell’11%. Se, anzichè calcolare il valore attuale con sconto commerciale si calcolasse il valore attuale con sconto composto, a quale tasso occorrerebbe scontare per avere lo stesso risultato di prima?

Sconto composto

1) Calcola il valore attuale con sconto composto del capitale di 1320€, che scade fra 5 anni, al tasso del 6%.

2) Calcola il valore attuale con sconto composto al 5,2% del capitale di 2160€ esigibile fra 11 anni.

3) Calcola il valore attuale con sconto composto al 7,35% del capitale di 3400€, che scade fra 8 anni.

L’ultima tipologia di sconto è quello composto che, come dice il nome stesso,  fa riferimento al relativo interesse.

Nell’interesse composto ho:

La formula riassuntiva dello sconto composto è:

Dividendo entrambi i membri per mi trovo il valore attuale

applicando la definizione di sconto ()

1) Applico lo sconto semplice, calcola il valore attuale al tasso del 6% di un capitale di 400€ con scadenza di 2 anni .

2) Sempre con sconto semplice, ho un tasso del 5,39%, calcola il valore attuale per un capitale di 3600€ che scade tra 3 anni e 6 mesi.

3) Sempre con sconto semplice, si calcoli il valore attuale al tasso del 7,25% di un capitale di 420€ che scade tra 8 mesi e 10 giorni.

4) Sempre con sconto semplice, calcolare il valore attuale con sconto semplice al tasso del 5,8% di un capitale di 980€ esigibile tra 1 anno 3 mesi e 25 giorni.

Adesso un esercizio leggermente più difficile:

5) Cacolare quale tasso è stato applicato nel caso in cui si abbia un capitale di 500€ con scadenza tra 2 anni, 4 mesi, dietro ad un incasso (valore attuale) di 468,34€.

Nello sconto commerciale si fa un grande richiamo all’interesse semplice.

Nell’interesse semplice si aveva che M = C (1 + it) dove con M si identifica il capitale aumentato dell’interesse ossia il montante.

Nello sconto semplice invece che pensare ad M penso a C per cui applicando la formula in maniera uguale ho:

C = V(1 + it)

La formual inversa (vedasi argomento sulle equazioni di I grado) divido sia a destra che a sinistra per (1 + it) ed ho che

(1)       V = C / (1 + it)

Ricordando che:

S = C – V

sostituendo la (1) nella S = C- V ed applicando il minimo comune multiplo tra binomi (aiuto?????) posso dire che:

S = Cit / (1+ it)

Ecco i passaggi per arrivare alla formula precedente:

spiegazione

Altre formule inverse necessarie allo sviluppo degli esercizi.

Partendo dalla (1) devo trovare il tasso o il tempo.

Moltiplico a sinistra e a destra per (1+i*t) ed avrò:

C = V(1 + i*t) = V + V*i*t

V*i*t = C -V

t = C-V / V*i

oppure

i = C-V /V*t

A questo punto ho tutte le formule.