Carlo Carrà
Le equazioni di primo grado si possono risolvere sempre utilizzando la seguente regola fondamentale che nasce dal pensare un’equazione ai due bracci di una bilancia:
quello che faccio al membro di sinistra (o braccio sinistro della bilancia) deve sempre essere fatto al membro di destra (o braccio destro della bilancia).
Se
7 = 7
allora posso sommare a destra e sinistra lo stesso numero (3) ed il risultato non cambia:
7 + 3 = 7 + 3
posso dividere a destra e sinistra per lo stesso numero (3) ed il risultato non cambia:
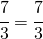
posso moltiplicare a destra e a sinistra per lo stesso numero (3) ed il risultato non cambia:
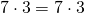
Partendo da questo presupposto posso risolvere la seguente equazione
x + 3 = 7
come?
REGOLA EMPIRICA (BUON SENSO!): LA X DEVE SEMPRE STARE DA SOLA E POSITIVA!
REGOLA PRIMA
Sommo a sinistra e a destra il -3 e risulta:
-3 + x +3 = 7-3
A questo punto -3 e +3 sono opposti e posso eliminarli:
A sinistra rimane la x da sola senza nessun coefficiente:
x = 4.
Questa è proprio la soluzione! Ossia vi è un solo numero che sostituito alla x e sommato al numero 3 fornisce proprio 7; infatti 4+3=7.
Questa regola viene spesso applicata dicendo che quando il numero passa il simbolo di uguale esso cambia di segno ossia da positivo diventa negativo e da negativo diventa positivo: è ciò che si vede ma in realtà ciò che accade è che si è sommata la stessa cifra a destra e a sinistra dell’uguale e siccome a sinistra vi è lo 0 (zero), sommandogli un numero si vede solo il numero stesso.
E’ come quando due oggetti uno caldo ed uno freddo si mettono a contatto, alla fine la temperatura dei due oggetti si equilibra; dal punto oggettivo si può pensare che il freddo sia passato da un oggetto all’altro ma ciò che accade è il corpo caldo che ha una maggiore energia riscalda il corpo freddo avvenendo un passaggio d’energia. Dal punto di vista pratico la temperatura dei due corpi si bilancia!
REGOLA SECONDA
Data l’equazione:
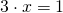
per applicare la REGOLA EMPIRICA devo moltiplicare a destra e a sinistra per 
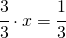
i due 3 si semplificano e come risultato ho: proprio:
CONCLUSIONE
La regola prima e la regola seconda con la regola empirica permettono di risolvere tutte le equazioni di primo grado
Fino ad ora ho citato solo l’interesse semplice. Per completare il discorso bisogna ribadire alcune cose e, naturalmente, anche le formule inverse che permettono di trovare tutto quello che si vuole a seconda dei campi di partenza.
.
Nel precedente post, sempre nella categoria matematica finanziaria avevo accennato al fatto della necessità di normalizzare la data rispetto al tasso.
Una delle prime cose che si studia sempre in matematica finanziaria è l’interesse semplice.
.
.
.
.
.
.