La tecnologia RFID è stata ed è oggetto di consistenti attività di normazione sia a livello pubblico (internazionale e regionale), sia privato (consorzi di aziende).
Una “libera” competizione (che quindi veda la competizione di specifiche tecniche di consorzi privati senza grande necessità di standard ufficiali emessi dalle organizzazioni di normativa), potrebbe essere vista come uno stimolo a sviluppare tecnologie antagoniste il cui successo sarebbe garantito dalle prestazioni e dal mercato invece che da accordi all’interno delle commissioni.
Le prime applicazioni, standardizzate tra il 1996 ed il 2001, sono quelle che riguardano il cosiddetto “closed loop”, ovvero i contesti in cui il medesimo TAG viene riusato per vari oggetti o, in logistica, nel caso di contenitori, in cui il TAG sia riusabile per contenuti differenti.
Gli esempi più celebri di applicazioni closed loop sono le carte senza contatto, per pagamenti e per controllo accessi, ma anche i TAG per lavanderia e quelli, già citati, per contenitori riusabili.
Per le applicazioni “closed loop” ISO ha sviluppato le famiglie di standard per carte senza contatto e per l’identificazione degli animali.
Le applicazioni cosiddette “open loop” riguardano l’uso degli RFID sui singoli oggetti nel commercio, ma anche gli RFID in contenitori “a perdere”(casse,imballaggi,pallet)eriusabili,qualii“container”,sedopo ogni viaggio, il TAG viene sostituito.
La progressiva riduzione dei costi dei TAG passivi sta rapidamente conducendo quest’ultimi dalle applicazioni “closed loop”, per le quali sononati,versonuoveapplicazioni “openloop”incuiilTAGvieneassociatononalcontenitoreriusabile,bensìalsingolooggetto,seguendoloper tutta la sua vita e spesso sopravvivendogli. Per questo tipo di applicazioni è previsto il maggior sviluppo in un prossimo futuro.
Organizzazioni pubbliche e consorzi di aziende hanno portato avanti, in questi anni, l’attività di normazione sui sistemi RFID; tra questi emergono essenzialmente EPCglobal ed ISO.
– EPC globalnato ed operante come una associazione privata.
-ISO (ed organismi ad esso collegati) che costituisce l’ente mondiale di normativa in quasi tutti i campi della tecnologia.
I primi standard RFID sono stati realizzati in ISO, per TAG passivi a bassa frequenza e comprendono:
– Gli standard sui TAG per identificazione degli animali
– ISO 11784
– Radio frequency identification of animals
– Code structure
– ISO 11785
– Radio frequency identification of animals
– Technical concept
– Protocolli per l’interfaccia radio per TAG RFID usati nei sistemi di pagamento, smart cards senza contatti e carte di prossimità
– ISO/IEC 10536 – Identification cards
— Contactless integrated circuit(s) cards
— ISO/IEC 14443
– Identification cards – Contactless integrated circuit(s) cards Proximity cards
– ISO/IEC 15693
– Identification cards
– Contactless integrated circuit(s) cards Vicinity cards
– Metodi per il test e la conformità di TAG e Reader RFID ad uno standard (ISO/IEC 18047);
– Metodi per il test delle prestazioni di TAG e Reader RFID (ISO/IEC 18046). Successivamente EPCglobal ha prodotto normative orientate all’uso dei TAG nella logistica, ovvero:
• una tassonomia di classi di TAG;
• standard per protocolli di comunicazione a radio frequenza tra TAG e Reader;
• formato per la memorizzazione delle informazioni di identificazione nei TAG.
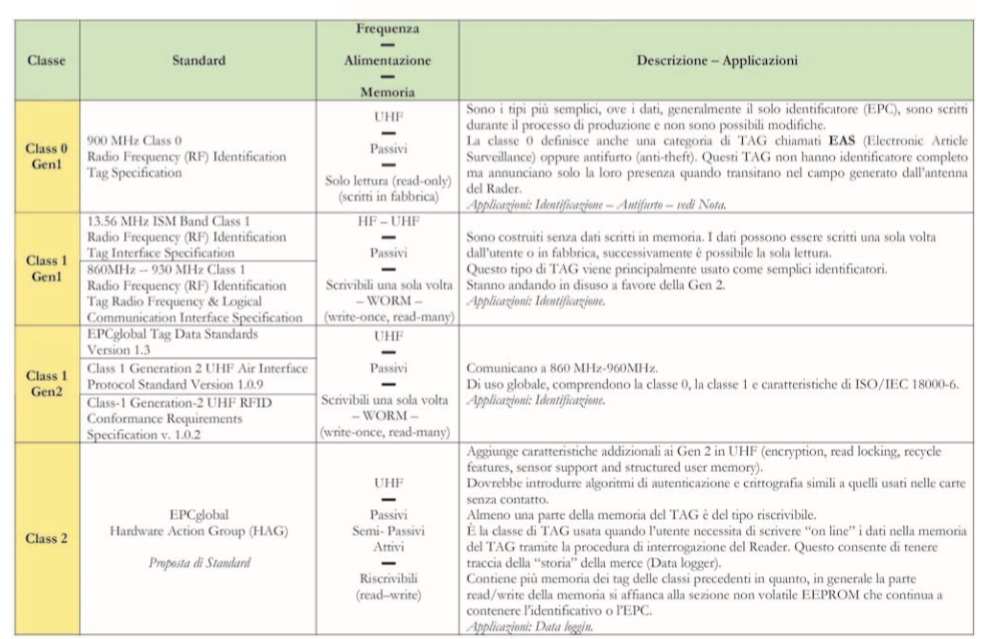
STANDARD EPCGLOBAL E LORO EVOLUZIONE
Vengono comunemente considerate altre tre classi di TAG, entrambe relative ad apparati attivi o semi-passivi: – Classe 3 – READ/WRITE – TAG semi-passivi – con sensori a bordo Applicazioni:
Data loggin
Questa classe, in aggiunta alle prestazioni della classe precedente, contiene, a bordo sensori e logica di controllo dei medesimi. I sensori più diffusi sono relativi alla pressione, moto o temperatura (i più diffusi in assoluto, per le esigenze logistiche della“catena del freddo”). Se la logica di controllo dei sensori lo permette, questi possono essere letti e
registrati in memoria anche senza l’intervento del Reader che, quando interrogherà il TAG si vedrà restituita anche la storia delle grandezze misurate. Naturalmente la complessità circuitale ed il relativo consumo di energia richiedono TAG attivi o almeno semi-passivi.
Classe 4 – READ/WRITE – con trasmittente a bordo – Network Capabilities – Applicazioni: Ad-Hoc Network; Active wireless sensor network Questa classe di TAG, con trasmettitore a bordo, si comporta come un sistema dotato di logica autonoma, potendo comunicare da TAG a TAG senza la presenza del Reader. In questi casi non solo si è in presenza di TAG attivi, ma l’attività, e di conseguenza l’erogazione di energia dalla batteria, permane anche in assenza di interrogazioni da parte del Reader. Per il resto sono previste tutte le prestazioni della classe 3.
– Classe 5 – READ/WRITE – con trasmittente a bordo – Network Capabilities. Oltre alla caratteristiche della classe 4 si ipotizza la possibilità di colloquio con TAG passivi, con funzionalità del tipo di quelle degli NFC
• Modulazioni & Codifiche
Lo standard prevede l’impiego da parte del TAG delle modulazioni ASK e PSK in modo indifferente (non esistono comandi di selezione ed i Reader devono ricevere entrambi). La PSK è stata inclusa perché massimizza il trasferimento di energia (utile nel verso Reader=>TAG) e presenta migliori caratteristiche di robustezza al rumore (utile nel verso TAG=>Reader). Le codifiche di linea previste sono FM0 o Miller con generazione di sottoportante attraverso il parametro M. Da parte del Reader possono essere impiegate DSB-ASK opp. SSBASK oppure PR-ASK con indice di modulazione del 90% e con codifica di linea PIE.
• Memoria
Lo standard prevede una capacità di memoria non troppo dissimile dai TAG di classe 1 (EPCglobal). Da 96 a 512 bit di memoria nel TAG contro i precedenti 64÷96 (comunque sufficienti a contenere l’EPC). L’aspetto più interessante consiste nella segmentazione della memoria per contenere maggiori informazioni rispetto al semplice EPC e nella protezione (per segmenti) della memoria di cui si vedrà in seguito.
Bitrate vs. identificazione dei TAG
In genere si riconosce ai TAG Gen2 una velocità superiore alle generazioni precedenti. I bitrate ammessi sono Reader =>TAG 26,7÷128 kbit/s; TAG=>Reader 5÷640 kbit/s. I bitrate vengono gestiti dal Reader nelmomento in cui il TAG viene letto/scritto per ottimizzare la velocità di riconoscimento di TAG con l’affidabilità di trasmissione. Infatti con bitrate alti si aumenta la velocità dell’algoritmo anticollisione, accelerando il riconoscimento dei TAG. Con bitrate bassi si favorisce la robustezza del segnale verso il rumore. Nel verso TAG=>Reader vengono usati 40÷640 kbit/s con codifica FM0 e 5÷320 kbit/s con codifica Miller. La velocità di lettura è funzione di diverse variabili che comprendono la potenza d’uscita, la densità dei TAG e l’ambiente operativo a radiofrequenza. Le specifiche Gen2 dovrebbero consentire ai Reader di effettuare, con circa 250 TAG nel raggio di copertura, circa 1500 letture di TAG al secondo in Nord America, e 600 letture per secondo in Europa, dove la potenza irradiata, la banda e il “Duty Cycle” hanno limiti più stretti. Queste velocità di lettura supportano la capacità di identificare oggetti su nastri trasportatori in movimento o trasportati da carrelli elevatori in transito attraverso portali di lettura con velocità anche superiori ai 10 Km/h.
Efficienza spettrale
Vengono definiti tre modi operativi per i sistemi RFID: Reader singolo, Reader multipli, Reader multipli ad elevata densità. Le specifiche per i Reader che operano in ciascuno di tali ambienti sono state concepite per fornire prestazioni maggiori rispetto a quelli esistenti. I TAG Gen2 possono essere letti e scritti da Reader di ognuna delle categorie precedentemente elencate. La modalità operativa di Reader multipli ad elevata densità è la scelta più affidabile ma di maggior complessità; consente un uso efficiente della banda, ottimizza le prestazioni e protegge dalle interferenze.
Affidabilità
Sono previsti miglioramenti essenziali rispetto ai precedenti. Le nuove caratteristiche mirano all’eliminazione di falsi positivi in lettura e in generale all’ottenimento di maggiore affidabilità nella lettura medesima. Vi è anche la possibilità di introdurre meccanismi per incrementare le prestazioni in termini di integrità dei dati. Ad esempio è possibile la verifica, dopo scrittura, dei dati in memoria del TAG (opzionale da parte del Reader).
Raggio di copertura
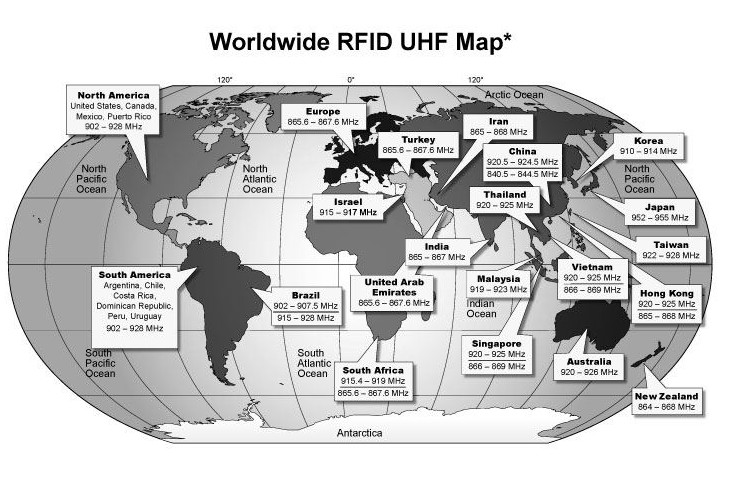
Lo standard Gen2 consente ma non obbliga l’uso di tecniche di Frequency Hopping prevedendo canali di 500 kHz nella banda assegnata negli USA (da 902,5 a 927,5 MHz). Tecniche alternative (Listen Before Talk – LBT) in uso in Europa possono prevedere un “Duty Cycle” più breve e operare con meno potenza, il che può comportare maggiore lentezza di lettura e un raggio di copertura ridotto. Bisogna comunque ricordare che il massimo raggio di copertura è principalmente funzione della potenza irradiata. Poiché i limiti per tale potenzasonodifferentipergliUSA,l’EuropaeilGiappone,cisidovrà aspettare valori differenti tra queste aree (in particolare i valori massimi in USA sono maggiori rispetto a quelli in Europa e Giappone)
Sicurezza
I TAG conformi allo standard Gen2 sono protetti da manomissioni. Il cosiddetto “cloaking”, infatti, consente di configurare i TAG in modo tale che prima di rispondere a qualunque interrogazione necessitano di ricevere una password dal Reader. Password possono essere anche richieste per scrivere i TAG o disabilitarli. Altro requisito di sicurezza supportato dallo standard e particolarmente richiesto è la possibilità di disabilitare definitivamente (“killing”) i TAG in modo tale che i loro dati non possano più essere accessibili. Questo è un requisito essenziale nell’ambito della vendita al dettaglio al fine di dissipare i timori dei consumatori riguardo la loro privacy. Sono definite password separate (a 32 bit) per il killing, per il cloaking, o per accedere alle diverse sezioni della memoria dei TAG.