SCIENZE E TECNOLOGIE INFORMATICHE

[:it]

Giuseppe Borsato

Prima di tutto con il comando

su

si diventa root.

Con il comando

exit

si torna utente.

Si possono aggiungere gli utenti e gestire i gruppi solo quando si è root.

Prima di tutto si aggiunge un gruppo:

addgroup programmatori

con il comando:

cat /etc/group

vedo la lista dei gruppi:

Adesso aggiungo un utente alla lista dei programmatori con il comando:

useradd -G programmatori marcello

con il comando

cat /etc/group |grep marcello

questo comando fa vedere il contenuto del file di configurazione group presente nella directory etc

vedo a quali gruppi appartiene l’utente marcello

Si può anche usare il comando

groups marcello

Da notare alcune cose molto importanti.

con il comando -G maiuscolo ho creato un utente assegnandoli un gruppo ma il sistema deve assegnare ogni utente ad un gruppo primario. Siccome in questo caso ho semplicemente specificato -G ossia l’associazione del mio utente al gruppo secondario, il mio sistema ha creato anche il gruppo primario marcello.

E’ cosa buona questa?

In realtà la cosa migliore è sempre creare un gruppo primario e poi i vari gruppi secondari a cui associare i vari utenti.

Il gruppo primario è quello che viene usato quando creiamo un file, che diventa anche il gruppo proprietario del file.

I gruppi secondari sono quelli che vengono controllati, oltre a quello primario, quando vogliamo accedere ad un file o ad una risorsa di cui non siamo proprietari.

Per aggiungere la password all’utente marcello si deve usare il comando:

passwd marcello

il sistema chiederà due volte l’inserimento della password.

Per cancellare un utente si usa il comando

deluser marcello

Per aggiungere un utente ad un gruppo si usa il comando:

adduser nomeutente nomegruppo 

ade sempio adduser francesco programmatori

se ho creato un gruppo primario (che deve esistere) e devo creare un nuovo utente devo usare  il comando

adduser -g gruppoprimario -G grupposecondario nomeutente

se poi voglio cancellare il gruppo primario senza aver prima cancellato o spostato tutti gli utenti del gruppo primario il sistema mi fornisce un messaggio:

Se invece cancello il gruppo secondario posso farlo senza problemi come si vede nella videata precedente.

Per cambiare utente si usa il comando

su nomeutente

NOTA FINALE

adduser crea una directory home per l’utente, la popola con il contenuto di / etc / skel e consente di impostare la password in modo interattivo.[:]

[:it]

Eugene Delacroix

Il firewall è uno strumento che è in grado di analizzare il traffico di rete e di gestirlo in base a regole predefinite, può essere un programma software oppure un componente hardware dedicato.

Tutto il traffico di una rete è formato da pacchetti.

Un pacchetto possiede un’intestazione (header) che contiene le informazioni sul pacchetto (indirizzo del mittente, indirizzo di destinazione, porta, ecc.) e un corpo (body) che contiene le informazioni da trasmettere.

Il firewall decide se bloccare o lasciare transitare ogni pacchetto

• a seconda delle informazioni contenute nell’header
• la porta sorgente o di destinazione

Quindi avviene un packet filter

Tramite il componente Netfiler si realizzano tutte le componenti avanzate del firewall. Lo strumento per manipolare netfilter si chiama Iptables.

Il sistema netfilter è basato su regole raggruppate in catene (chain), a loro volta raggruppate in tabelle (tables).

Ogni tabella definisce un tipo diverso di operazioni che è possibile effettuare sui pacchetti; ogni catena definisce come vengono trattati i pacchetti nelle diverse fasi della loro elaborazione.

Le tabelle in considerazione sono:

tabella filtro (filter): è responsabile del filtraggio dei pacchetti, permette cioè di bloccarli o di farli passare. Ogni pacchetto passa attraverso la tabella filtro. Essa contiene le seguenti catene predefinite:

• catena INPUT: tutti i pacchetti destinati al sistema passano attraverso questa catena.
• catena OUTPUT: tutti i pacchetti creati dal sistema passano attraverso questa catena.
• catena FORWARD: tutti i pacchetti che hanno come destinazione finale un altro sistema e che non sono stati generati dal sistema stesso, cioè tutti i pacchetti che vengono meramente instradati dal sistema, passano attraverso questa catena.

tabella nat: questa tabella è responsabile dell’impostazione delle regole per la modifica degli indirizzi e porte dei pacchetti. Il primo pacchetto di una connessione passa attraverso questa tabella, e il risultato del passaggio del primo pacchetto determina come tutti gli altri pacchetti della stessa connessione verranno modificati. La tabella nat contiene le seguenti catene predefinite:

• catena PREROUTING: passano attraverso questa catena i pacchetti in entrata, il passaggio avviene prima che la locale tabella di routing venga consultata per effettuare l’instradamento. Essa è usata per il NAT sulla destinazione o DNAT.
• catena POSTROUTING: passano attraverso questa catena i pacchetti in uscita dopo che la locale tabella di routing sia stata consultata. Usata per il NAT sulla sorgente o SNAT.
• catena OUTPUT: permette un DNAT limitato sui pacchetti generati localmente.

tabella mangle: questa tabella è responsabile delle modifiche alle opzioni dei pacchetti, come ad esempio quella che determina la qualità del servizio. Tutti i pacchetti passano attraverso questa tabella. Essa contiene tutte le catene predefinite:

• catena PREROUTING: esamina tutti i pacchetti che in qualche modo entrano nel sistema. Questo processo avviene prima che il routing decida se il pacchetto debba essere inoltrato (catena FORWARD) o se sia destinato al sistema. Viene utilizzata per manipolare l’header del pacchetto (catena INPUT).
• catena INPUT: tutti i pacchetti destinati al sistema passano per questa catena.
• catena FORWARD: tutti i pacchetti che vengono instradati dal sistema ma di cui il sistema non è né sorgente iniziale né destinazione finale, passano per questa catena.
• catena OUTPUT: tutti i pacchetti generati dal sistema passano per questa catena.
• catena POSTROUTING: tutti i pacchetti che lasciano il sistema, sia quelli in OUTPUT sia quelli in FORWARD, passano poi per questa catena.

tabella raw: questa tabella, introdotta ufficialmente nel corso dello sviluppo della serie 2.6 del kernel, ha lo scopo di evitare il connection tracking per quei pacchetti che, per una qualche ragione, non si vogliono filtrare in maniera stateful. Le catene previste per la tabella raw sono solo due:

• catena OUTPUT: in tale catena si andrà ad operare sui pacchetti generati da processi locali.
• catena PREROUTING: in tale catena si andrà, invece, ad operare sui pacchetti provenienti da qualsiasi interfaccia di rete.

La tabella di default è la tabella filter.

Al termine di ogni catena vi è la politica ACCEPT ossia un pacchetto raggiunge la fine della catena e viene accettato.

ESEMPIO

Si consideri il comando

ossia il comando

sudo iptables -A INPUT -p udp -j DROP

per cancellare la regola ho usato il comando

sudo iptables -F

Non avendo specificato alcun indirizzo, né del mittente né del destinatario, viene mostrata la dicitura anywhere.
Le seguenti opzioni consentono di aggiungere, modificare o eliminare determinate regole di una catena:
-A nome_catena
aggiunge una regola in fondo alla catena indicata (append);
-D nome_catena numero_regola
rimuove la regola dalla catena indicata (delete);
-L nome_catena
mostra l’elenco delle regole della catena (senza opzioni mostra le tre catene della tabella filter);
-F nome_catena
svuota una catena (senza opzioni svuota le tre catene della tabella filter).

Le opzioni per descrivere il pacchetto permettono di specificare:
–p il protocollo
–s l’indirizzo IP sorgente
–d l’indirizzo IP destinatario
–i l’interfaccia
–g la catena da attraversare successivamente
–t la tabella (senza alcuna opzione viene usata la tabella filter).

Per esempio, il seguente comando blocca ogni tipo di pacchetto in uscita verso un particolare indirizzo IP (per esempio 123.12.13.12):

sudo iptables –A OUTPUT –d 123.12.13.12 –j DROP

Per bloccare qualsiasi connessione sulla porta 22, proveniente dall’esterno, si deve scrivere il comando:

sudo iptables –A INPUT –p 22 –j DROP

Per impostare il sistema in modo che non venga fornita risposta al comando ping inviato ad una particolare interfaccia di rete (per esempio eth0) si deve utilizzare il comando seguente:

sudo iptables –A INPUT -i eth0 –p icmp –j DROP

Si consideri un altro esempio rappresentato dalla seguente situazione: si supponga di essere connessi alla rete Internet tramite l’interfaccia di rete ppp0 e di avere avviato un server FTP per il trasferimento di file nella rete locale. Per evitare che vi siano dall’esterno, cioè da Internet, connessioni non desiderate di tipo FTP, che utilizzano la porta 21, si deve scrivere il seguente comando:
sudo iptables –A INPUT –p 21 –i ppp0 –j DROP

Analogamente, nel caso di un server Web locale, si può bloccare la porta 80 con il comando seguente:

sudo iptables –A INPUT –p 80 –i ppp0 –j DROP

 [:]

[:it]

Jackson Pollock

[WpProQuiz 58][:]

[:it]

Dorothea Tanning

Il proxy server

Il proxy server è un servizio, che si attiva per motivi di sicurezza e di efficienza della rete stessa, tra client e server evitando connessioni dirette tra i due.

Con tale servizio,

i client inviano le richieste al proxy server

il proxy server le inoltra al server

raccoglie le risposte

e le invia ai client.

Un proxy server può essere utilizzato, ad esempio, per permettere a tutti i computer di una rete locale  di navigare in internet evitando però di effettuare connessioni, verso l’esterno della rete locale, che possono non essere sicure.

Esso può anche controllare le connessioni, impedendo la navigazione in determinati siti web.

In Linux il server proxy più utilizzato si chiama squid

Per installarlo il comando da utilizzare è:

sudo   apt-get install  squid

per avviarlo (da utente amministratore):

sudo   /etc/init.d/squid  start

Il file di configurazione si chiama

/etc/squid/squid.conf

Su di esso vanno fatte delle modifiche e successivamente riavviato il server con il comando:

sudo   /etc/init.d/squid  restart

MODIFICHE

Specificare

una porta per il server,

ad esempio la 3128,

togliendo il carattere # (che indica un commento) alla riga

http_port   3128

sudo   /etc/init.d/squid  start

i file di log,

i parametri amministrativi (mail del gestore del servizio, l’hostname ed altri)

la lista ACL (Access Control List) di chi può accedere al servizio :

ogni riga della ACL è composta dai seguenti campi

acl          nome                    tipo        regola                   opzione1             opzione2             …….

Esempio

Acl          retelocale           src          192.168.0.0/255.255.255.0

Tale impostazione consente l’accesso al proxy da ogni host del  tipo       192.168.0.x

Per abilitare la lista ACL occorre inserire la riga seguente:

http_access allow            retelocale

che permette alla lista retelocale l’accesso http.

Per negare questo tipo di accesso occorre scrivere la seguente riga:

http_access deny            retelocale[:]

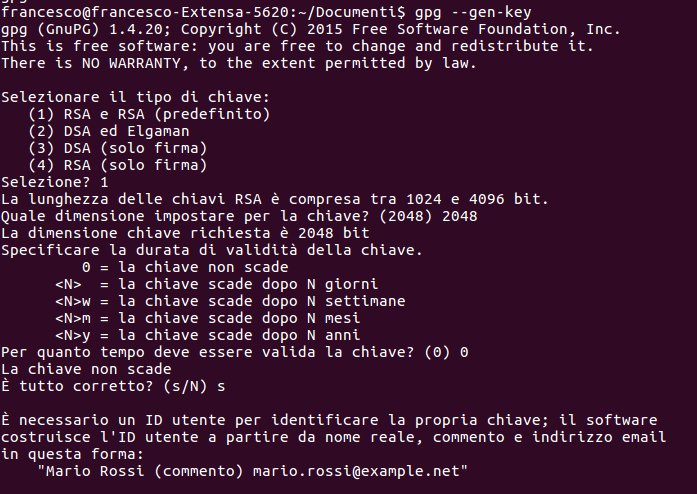
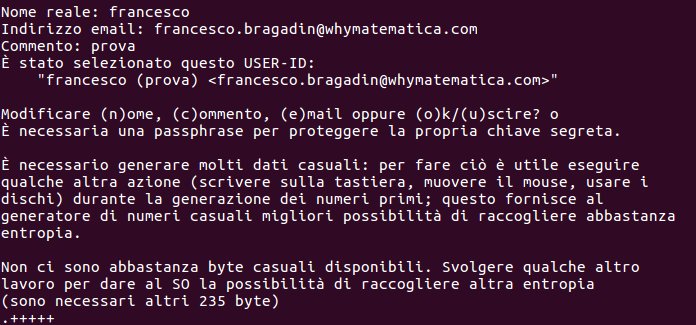
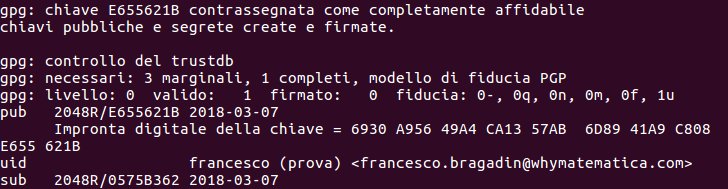
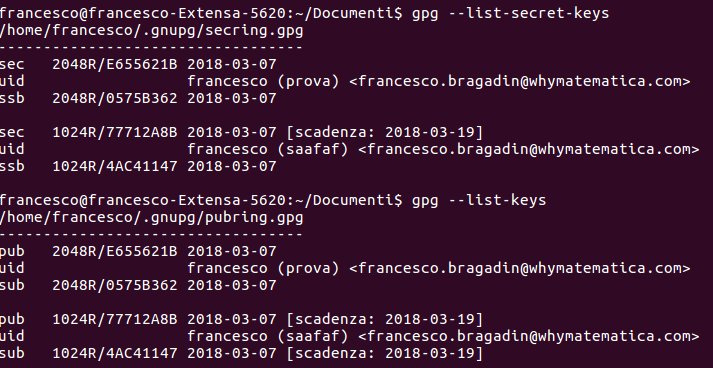
[:it]

Jackson Pollock

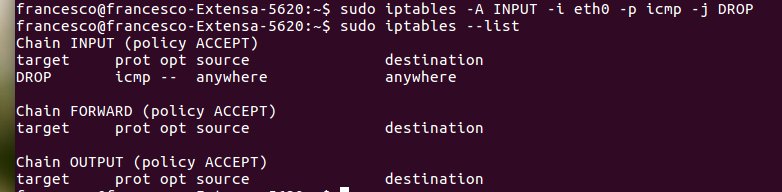
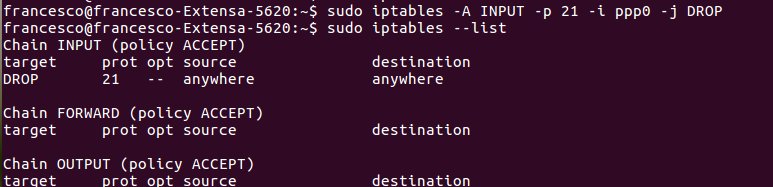
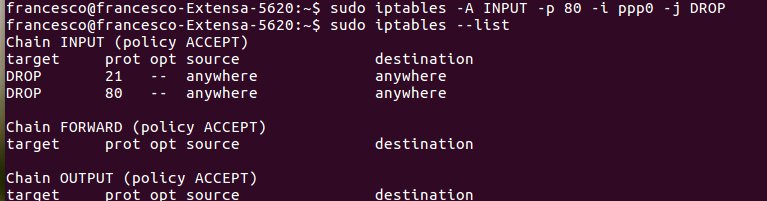
In Linux si può utilizzare

il protocollo NFS per la condivisione di porzioni di filesystem,

il protocollo CUPS per la condivisione di stampanti

OPPURE

si può utilizzare samba che permette di condividere file e stampanti in reti miste ossia reti formate da computer con sistemi operativi differenti.

NFS

Il protocollo NFS (Network File System) permette di montare in modo semplice il filesystem di un sistema remoto. In questo modo è possibile visualizzare, modificare o eliminare file che si trovano su un computer remoto come se fossero disponibili sul computer locale. Questo sistema ha due aspetti negativi:
– il protocollo presenta una sicurezza limitata;
– non è compatibile con i sistemi Windows.
Tuttavia può essere utile quando si ha la necessità di condividere dati in una rete locale
considerata sicura e composta da computer con sistema operativo Linux.
Il computer che condivide i dati è il server NFS, sul quale sono attivi i demoni mountd e nfsd, mentre gli utenti utilizzano il client NFS.

Un server samba svolge le seguenti funzioni:

• dal lato server permette di avere un computer Linux che svolge le stesse funzioni di

file server o print server Windows

cioè può mettere a disposizione le proprie risorse a computer client aventi sistemi operativi differenti

• dal lato client permette di utilizzare le risorse condivise da un file server o print server Windows

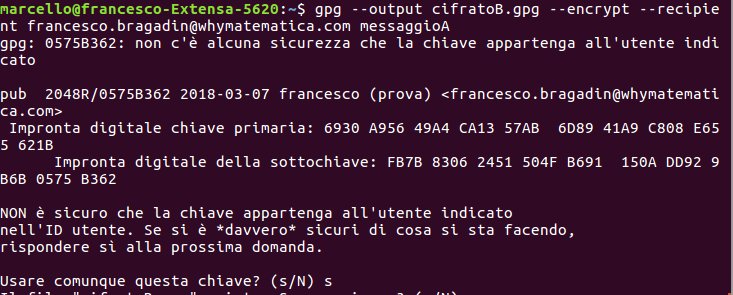
CONDIVIDERE LE RISORSE CON UN SERVER SAMBA

Dal punto di vista del computer client, il servizio smbclient si integra con il file manager dell’interfaccia grafica di Linux.

Per visualizzare l’elenco delle risorse messe a disposizione da un computer si puo’ aprire il file manager e scrivere nella barra degli indirizzi la seguente riga:

smb://indirizzoIP

dove indirizzoIP va sostituito con l’effettivo indirizzoIP del computer che mette a disposizione le risorse.

Per esempio in Ubuntu, si deve aprire la finestra di File:

nel menu File, scegliere Inserisciposizione

e scrivere nella casella in alto:

smb://indirizzoIP

Se invece si scrive solo

smb://

si può navigare attraverso i computer della rete in modo analogo a Risorse di rete in un sistema Windows.

dal lato server è necessario invece avviare due demoni

smbd  (demone di samba)

e

nmbd (demone per il netBios, un servizio simile a DNS).

ENTRAMBI i servizi possono essere avviati con il seguente comando:

sudo  /etc/init.d/samba  start

Il demone utilizza il file di configurazione

/etc/samba/smb.conf

Esso contiene tutte le informazioni sia sulle risorse condivise che sulle autorizzazioni necessarie per l’utilizzo di tali risorse.

In questo file di configurazioni, i commenti sono contrassegnati dal ; iniziale

Questo file di configurazione è diviso in sezioni, il nome delle sezioni è indicato tra parentesi […..]

Analizziamo le sezioni

[global],  [homes] e [tmp].

La sezione [global]

Definisce le impostazioni comuni per ogni risorsa ed ha al suo interno le seguenti specifiche:

[global]                                                          CHE DEFINISCONO:

printing = cups                                               => l’uso di cups per la gestione delle stampanti

printcap name = cups                        =>                    “

load printers = yes                                         => permette la condivisione delle stampanti

guest account = nobody                                 => autorizza il generico utente (nobody)

invalid users = root                                        => disabilita l’utente root per motivi di sicurezza

workgroup = WORKGROUP                           => assegna il nome del workgroup (gruppo di lavoro a cui appartiene il computer, in una rete infatti possono essere presenti piu gruppi di lavoro

[homes]

comment = Directory Personali

browseable = no

read only = no

create mode = 0750

vengono condivise le directory home, con permesso di scrittura, ogni utente può visualizzare solo la propria directory.

I permessi dei files sono impostati su 0750.

[tmp]

comment = qui si possono mettere i files temporanei

path  = /tmp                                                   per indicare il percorso delle risorse

read only  = no

public = yes

la sezione [tmp] imposta una directory che conterrà i files temporanei,

specifica inoltre, l’accesso pubblico in scrittura.

Con queste impostazioni, il server mette in condivisione le stampanti e tutte le home directory.

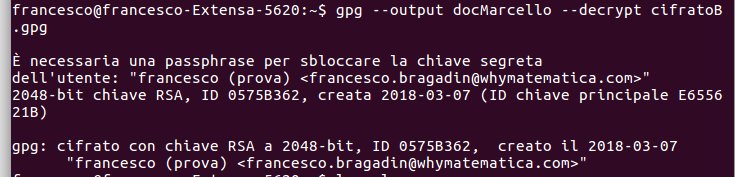
Resta da definire in ultimo, con il seguente comando, una password per gli utenti:

smbpasswd studente1

New SMB password:  ………………………

Retype new SMB password: ……………

In questo modo l’utente studente1 può visualizzare la propria home anche da un computer Windows.[:]

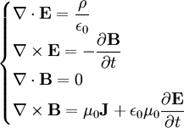[:it]La teoria del campo elettromagnetico è sintetizzata in quattro leggi. Esse sono chiamate equazioni di Maxwell poiché fu Maxwell che, oltre a formulare la quarta legge, comprese che esse costituiscono il fondamento essenziale della teoria delle iterazioni elettromagnetiche.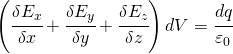

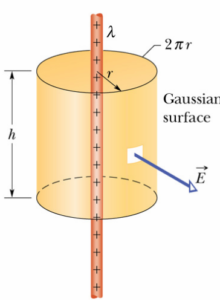La prima equazione di maxwell è la legge di Gauss per il campo elettrico.

Oltre che esprimerla in forma integrale:

si può esprimere in forma differenziale.

.

Considerando una variazione infinitesima di campo elettrico lungo una direzione la relazione precedente diventa:

Considerando le tre dimensioni e derivando la relazione iniziale:

si ha:

ossia:

con densità di carica volumetrica.

In termini matematici si può scrivere:

ossia la divergenza del vettore campo elettrico è uguale alla densità di carica volumetrica divisa la costante dielettrica nel vuoto.[:]

[:it]Campo elettrico di una lastra carica infinitamente estesa

con superficie della base della lastra.

per cui:

concludendo:

con densità di carica superficiale.

Nel caso di un condensatore che è formato da due piastre caricate con cariche opposte il campo elettrico all’interno delle due piastre vale:

il campo elettrico di un condensatore all’esterno è nullo in quanto i campi elettrici all’esterno si sottraggono mentre si sommano all’interno.

Campo elettrico di un filo carico infinitamente lungo

con base del cilindro (filo) e lunghezza del filo.

unendo le due realzioni:

da cui:

con

densità lineare di carica.

Quindi il campo elettrico prodotto da un cavo diminuisce in maniera inversamente proporzionale alla distanza.

Nel caso in cui si inserisse un dielettrico aumenta il denominatore.[:]

[:it]Si consideri una carica puntiforme e si calcoli il flusso del campo elettrico   da essa prodotta attraverso una superficie sferica avente il centro coincidente con la carica.

Il flusso, in generale, è il calcolo della quantità che attraversa una superficie chiusa.

Si divide la superficie in superfici molto piccole (o infinitesime) di aree , , ,…Su ciascuna di esse si può disegnare un vettore unitario , ,,…perpendicolare alla superficie in quel punto.

Siano , , ,… (theta) gli angoli tra i vettori normali , ,,…e i vettori del campo , , ,… in ogni punto della superficie.

Allora il flusso del campo vettoriale attraverso la superficie S è:

sapendo che
il flusso può essere scritto come:

ma sapendo cheil prodotto di una base per un’altezza mi fornisce proprio un integrale la realazione precedente può essere scritta come:

dove il segno di circoletto sull’integrale significa che è superficie chiusa.

Tutta questa premessa è servita per applicarla al campo elettrico.

Si calcola il flusso del campo elettrico attraverso una superficie sferica.

Il vettore unitario normale ad una sfera coincide con il vettore unitario lungo la direzione radiale .

Perciò l’angolo fra il campo elettrico e il vettore unitario normale è nullo e .

Il campo elettrico ha lo stesso valore in tutti i punti della superficie sferica e che l’area della sfera è  .

Il valore del flusso del campo elettrico risulta:

concludendo

La legge di Gauss è particolarmente utile quando si vuole calcolare il campo elettrico prodotto da distribuzioni di carica aventi determinate simmetrie geometriche ad esempio piastre, sfere, o fili percorsi da corrente.[:]

[:it]

Christian Lassen Reise

[WpProQuiz 57][:]

[:it]TEMA 1.
Si continui ad inserire una coppia di numeri interi finchè non si inserisce quella che rappresenta l’origine degli assi cartesiani o una coordinata è nulla. Ogni coppia rappresenta un punto.

Si memorizzino solo la prima coppia e l’ultima inserita.

Si definisca una funzione che calcoli la distanza tra i due punti  usando la formula della distanza. (si inserisca la funzione import math)

Si definisca la funzione che calcoli il valor medio tra i due punti.

Si mostri a video:

• i due punti
• la distanza tra i due punti
• il valor medio

TEMA 2

Si continui ad inserire una coppia di numeri interi finchè non si inserisce la coppia (1,2). Ogni coppia rappresenta un punto.

Si memorizzino solo la prima coppia e l’ultima inserita.

Si definisca una funzione che calcoli la distanza tra i due punti  usando la formula della distanza. (si inserisca la funzione import math)

Si definisca la funzione che calcoli il valor medio tra i due punti.

Si mostri a video:

• i due punti
• la distanza tra i due punti
• il valor medio

GRIGLIA DI VALUTAZIONE IN 100 esimi

[:]