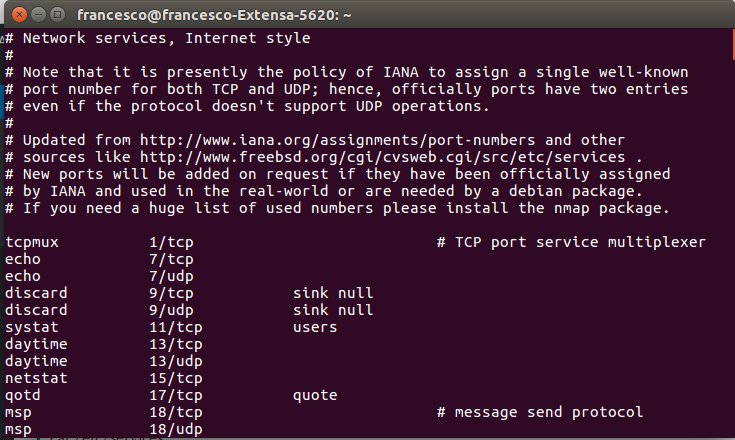
[:it]L’elenco delle porte è contenuto nelle file presente /etc/services
per visualizzarlo uso il comando
cat /etc/services
( per visualizzare il contenuto di un file si possono usare i comandi gedit o more o less, cat nasce principalmente per concatenare infatti deriva dall’inglese to cater = fornire)
per cercare una parola specifica all’interno di un file usare l’acronimo grep (general regular expression print)
cat /ets/services |grep www
quando un programma si attiva, il sistema assegna una porta. Il sistema si mette in listen (in ascolto)
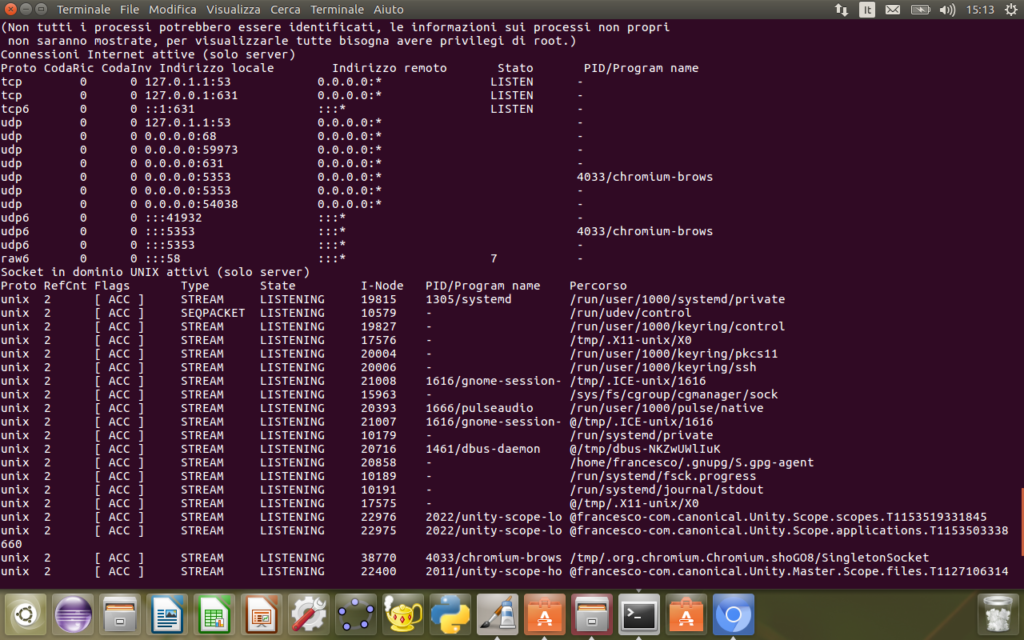
Per controllare le porte sulle quali avvengono le connessioni si utilizza il comando
netstat
con le relative opzioni
-l porte in ascolto
-n numero di porta
-p programma che utilizza quella porta
netstat -nlp
mostra le tre opzioni
il comando
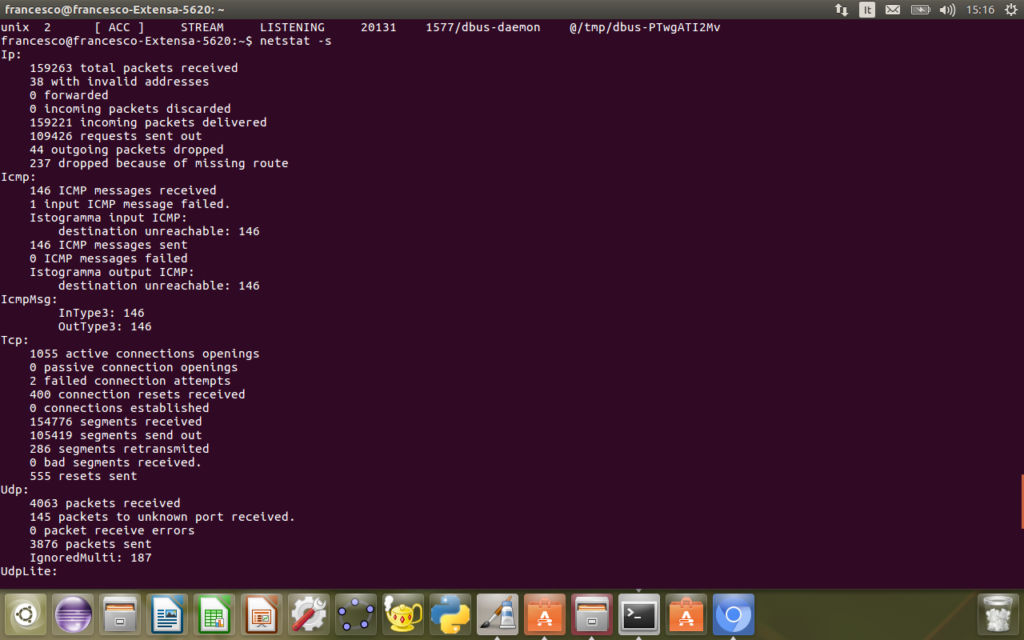
netstat -s
mostra il numero di pacchetti inviati, ricevuti, il numero di porte aperte, il numero di connessioni aperte
IFCONFIG
Serve per monitorare le interfacce di rete, attivarle o monitorarle
lo –> interfaccia di loopback
eth –> interfacce di rete Ethernet
sln –> interfacce di rete SLIP (linee seriali)
ppp –> dispositivi point to point Protocol
plip –> Parallel Line IP
il semplice comando
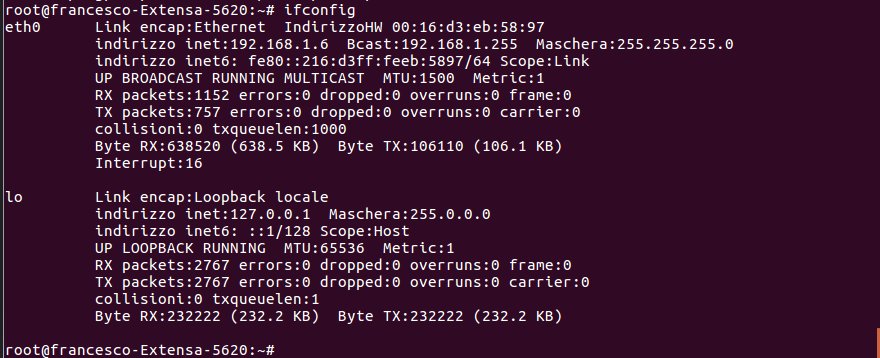
ifconfig
fornisce, ad esempio il seguente output:
Per attivare i meno un’interfaccia di rete si utilizza il comando:
ifconfig etho up
oppure
ifconfig etho down
con il seguente comando si associa un opportuno indirizzo di rete e netmask
ifconfig eth0 192.168.1.55 netmask 255.255.255.0[:]