SCIENZE E TECNOLOGIE INFORMATICHE

[:it]

Monet

Si chiama anche crittografia a chiave pubblica; si utilizzano due tipi di chiavi una pubblica ed una privata.

La codifica avviene con la chiave pubblica, la decodifica con quella privata.

L’utilizzo della coppia di chiavi determinano vari livelli di sicurezza:

Garanzia identità del mittente

Mittente A usa la chiave privata per codificare il messaggio–> Tutti i mittenti B usano la chiave pubblica del mittente per decifrare il messaggio

Tutti leggono il messaggio e viene garantita solo l’identità del mittente

Garanzia della segretezza

La chiave pubblica del destinatario è conosciuta e viene usata per codificare il messaggio, il mittente può decifrarlo perché usa la sua chiave privata.

In questo caso tutti possono codificare il messaggio con la chiave pubblica del destinatario ma non si ha la certezza del mittente. Il messaggio rimane comunque segreto perché solo chi è in possesso della chiave privata può decifrarlo

Garanzia della segretezza e del mittente

il mittente codifica con la sua chiave privata e viene codificato ancora con la chiave pubblica del destinatario, il destinatario usa la sua chiave privata per decodificare il messaggio  e lo decodifica con la chiave pubblica del mittente.

Il vantaggio del sistema crittografico a chiave asimmetrica è che il mittente e il destinatario non devono condividere una chiave segreta. I mittenti dei messaggi devono solo conoscere la chiave pubblica del destinatario, mentre la chiave privata deve essere conservata in modo segreto dal destinatario.

La chiave privata e la chiave pubblica sono correlate mediante un opportuno algoritmo matematico.[:]

[:it]Questo brevissimo programma ha racchiuso il nucleo della gestione di funzioni con il linguaggio Python:

def area(a,b):
           c=a*b
          return c

f=input(“base”)
f=int(f)
g=input(“altezza”)
g=int(g)
d=area(f,g)
print (“area: “,d)

Da notare la sintassi per la definizione di finzione,

come essa viene chiamata.[:]

[:it]Calcolare tutte le date caratteristiche del CPM evidenziando il cammino critico.

Definire il CPM catalogandolo come grafo AON o AOA

TEMA 1

Tema 2

 [:]

[:it]

roger de la fresnaye

La cosa interessante è come si inizializza la lunghezza del vettore inserita a video:

v=new int[lung];

l’immissione dei dati può ovviamente avvenire all’interno di un ciclo:

import java.io.InputStreamReader;
import java.io.BufferedReader ;
import java.io.IOException;

public class Vettore {
public static void main(String[] args)

{
int v[],i,lung;
/*
* legge da tastiera la lunghezza del vettore
*/
lung =0;
BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
try {
lung = Integer.parseInt(input.readLine());
}
catch (Exception e) {
e.printStackTrace();
}

/* molto interessate la gestione delle lunghezza del vettore
*
*/

v=new int[lung];
v[1]= 1;
for (i=0;i<lung;i++)
{
v[i]=i;
}
for (i=0;i<lung;i++)
{
System.out.println(v[i]);
}

}}[:]

[:it]

roger de la fresnaye

Questo estratto permette l’inserimento di un carattere da tastiera e lo stampa a video:

System.out.println(“dammi una lettera”);
BufferedReader input2 = new BufferedReader(new InputStreamReader(System.in));
try {
char c = (char)input2.read();
System.out.println(“Hai scritto ‘”+c+”‘”);
}
catch (IOException e) {
e.printStackTrace();
}[:]

[:it]

roger de la fresnaye

Questo breve programma richiede in input una stringa per poi stamparla:

import java.io.InputStreamReader;
import java.io.BufferedReader ;
import java.io.IOException;

public class parola {
public static void main(String[] args ) {
     String x=null;
    System.out.println(“inseirsci una parola”);
       BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
try {
       x=input.readLine();
}
catch (Exception e) {
e.printStackTrace();
}
System.out.println(x);

}

}

si noti

• che a differenza dei dati numeri che devono essere sottoposti a modifica di tipo, Java legge sempre stringhe.
• le variabili definite all’interno del metodo main devono sempre essere inizializzate, nel caso specifico è messo a null.

con questa riga di codice si ha la lunghezza della stringa immessa:

lung=x.length();[:]

[:it]La funzione distribuzione di probabilità viene utilizzata per descrivere un fenomeno aleatorio (casuale) e fornire la probabilità che un certo evento accada o meno.

In particolare essa segue gli assiomi di Kolmogrov generalizzandoli.

La funzione distribuzione viene così definita:

conseguenza immediata è che:

che ricorda moltissimo il teorema del calcolo integrale ed il teorema di Torricelli-Barrow

Infatti si definisce la funzione densità di probabilità:

che comporta la seguente affermazione:

ossia la funzione densità di probabilità è la derivata della funzione distribuzione di probabilità o detto alla stessa maniera, la funzione distribuzione è l’integrale della funzione densità in un determinato intervallo.

Per chiarire immediatamente il concetto la funzione densità di probabilità più usata e conosciuta è la distribuzione di Gauss che descrive fenomeni aleatori continui che si concentrano verso un valore più probabile centrale.

La sua equazione è:

la forma della campana e il suo valore centrale dipendono dalla deviazione standard e dalla media .

Eccone un suo grafico:

Per capire la probabilità che una misura cada in un certo intervallo si deve calcolare l’area sottesa dalla curva in quell’intervallo ossia la sua funzione distribuzione o funzione primitiva negli intervalli presi in esame.[:]

[:it]La crittografia a chiave simmetrica utilizza la tessa chiave per cifrare e decifrare il messaggio.

Il cifrario a sostituzione è un esempio di crittografia a chiave simmetrica.

Un esempio di codifica e decodifica, utilizzando gli operatori logici è dato dalla codifica mediante una chiave ed effettuare un XOR sul messaggio di partenza, quindi effettuando un XOR mediante la stessa chiave sul messaggio trasmesso, ho il messaggio inviato ossia:

mi fornisce il messaggio codificato

quindi

Per comprendere adesso l’esempio consiglio di rivedere questi tre post

• operatori logici
• approfondimenti sugli operatori logici
• esercizi sugli operatori logici

Ad esempio invio il seguente messaggio:

Utilizzo la seguente chiave conosciuta sia dal mittente che dal destinatario:

Effettuo XOR tra il messaggio inviato e quello ricevuto ed ho trasmesso il seguente messaggio:

Adesso effettuo nuovamente XOR tra quest’ultimo e la chiave:

Il messaggio decifrato risulta quindi:

Approfondimenti

Più grande è la chiave più prove si devono effettuare per trovare il messaggio inviato.

Il numero di chiavi è sempre la disposizione con ripetizione ossia il numero di chiavi diverse è:

con il numero di bit della chiave.

Una persona che vuole decifrare il messaggio dovrà effettuare un numero esponenziale di prove.

Ad esempio:

• si usi una chiave lunga 40 bit
• si avranno chiavi diverse ossia circa chiavi diverse
• si supponga che si provi una chiave ogni millisecondo ossia secondi
• si pensi per capire l’operazione successiva al seguente esempio ossia si devono lavare tre auto e per ogni auto ci si impiega 10 minuti allora il tempo complessivo sarà , per lavare tre auto ci si impiega 30 minuti.
• applicando nel nostro caso si ha sapendo che in un giorno ci sono 86.400 secondi, dividendo la cifra con il numero di secondi risulta 11’574 giorni.
• supponiamo adesso di utilizzare un PC che provi chiavi in un secondo, esso impiegherà secondi ossia meno di tre ore per trovare la chiave.

Per determinare una chiave abbastanza sicura si usano infatti chiavi lunghe 128 bit.

I sistemi di crittografia a chiave simmetrica sono:

DES: Data Encryption Standard–> IBM 1977 utilizza un chiave a 56 bit (libro di approfondimento sul des)

Triple DES o 3 DES una chiave maggiore

CAST –> Nortel chiave a 128 bit

IDEA International Data Encryption Algorithm–> nel 1990 chiave a 128 bit[:]

[:it]

1. Costruire la tabella della verità associata al seguente circuito logico:

2. Costruire la tabella della verità associata al seguente circuito:

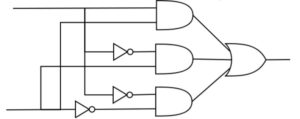
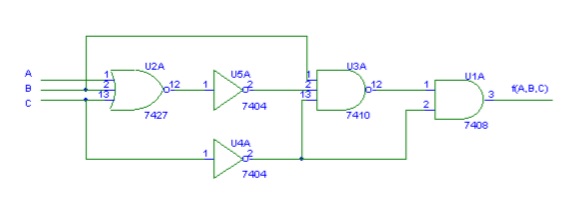
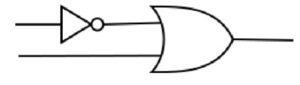3. Esercizi molto più complesso, associare la tabella di verità al seguente circuito:

 [:]