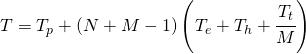[:it]

Jim Warren
Essendovi molti tipi diversi di hardware è nata l’esigenza di classificare e standardizzare i protocolli affinché hardware diversi ma anche software diversi potessero comunicare tra loro attraverso degli opportuni protocolli.
Conseguentemente un organismo si è fatto carico di fissare dei protocolli tale ente è:
ISO International Standard Organization
Nel 1984 è nata l’esigenza di fissare dei protocolli per le reti aperte per cui è nato
OSI Open System Interconnection
Assieme hanno dato vita al modello ISO/OSI
Si è utilizzato un approccio a layer (strati) che devono soddisfare le seguenti regole:
- a funzioni diverse per struttura logica o per tecnologia realizzativa devono corrispondere strati diversi e funzioni simile devono possibilmente essere inglobate nel medesimo strato
- le frontiere devono essere scelte in modo tale che sia possibile riprogettare la realizzazione dei singoli strati senza che vi sia la necessità di modificare gli strati adiacenti
- gli strati devono essere tali che le uniche iterazioni richieste avvengano soltatno con gli strati immediatamente adiacenti.
Sulla base di queste ed altre considerazioni, gli estensori del modello OSI sono giunti ad individuare 7 livelli o strati.
Tutti i protocolli necessari al corretto funzionamento dello strato 1: fisico e dello strato 2: collegamento dati, sono stati elaborati dal IEEE (Institute of Electrical and Electronics Engineers) col nome 802.
• 802.3 per le reti Ethernet
• 802.11 per le reti wireless standard
• 802.15 per le reti PAN (Personal Area Network) senza fili, per esempio le connessioni bluetooth
• 802.16 per le reti WiMAX, reti senza fili a banda larga.
Per gli altri strati, il protocollo è quello TCP/IP.
STRATO 7: strato di applicazione application layer
Due programmi di applicazione in sistemi diversi si comprendono a livello semantico, sicchè possono interagire. A livello semantico ossia il significato del codice è esattamente uguale a prescindere dal linguaggio adottato o dal dialetto utilizzato. Gestisce la posta elettronica, ad esempio sistemi diversi possono leggere la stessa posta.
STRATO 6: strato di presentazione presentation layer
Organizza i messaggi in modo che sistemi doversi possano comunicare a livello sintattico, cosicché le entità a livello 7 possono colloquiare preoccupandosi solo degli aspetti semantici e non di quelli sintattici. Questo strato può fornire i servizi di crittazione e decrittazione nonché servizi di compressione.
STRATO 5: strato di sessione session layer
Gestisce ogni singolo dialogo (sessione) instaurando il collegamento tra le entità 6 interessate, rilevando errori e cercando di correggerli, chiude la connessione al termine del collegamento.
STRATO 4: strato di trasporto transport layer
Fornisce il servizio di gestire il trasferimento fisico dei dati, a cominciare dalla loro organizzazione in unità di dati di dimensioni relativamente piccole (la cosiddetta pacchettizzazione). E’ questo lo strato che utilizza il servizio di trasmissione dei dati fornito dalla rete di comunicazione vera e propria: ne deriva che è proprio a questo livello che si possono valutare globalmente le prestazioni della rete stessa quali il traffico utile, il ritardo medio per la singola unità dati, la probabilità di errore residua,, la probabilità di collegamento.
STRATO 3: strato di rete network layer
Gestisce la trasmissione dei dati attraverso la rete di comunicazione, con particolare riferimento all’instradamento (routing).–> protocollo IP
STRATO 2: strato di collegamento dati data link layer
Fornisce canali di trasmissione il più possibile esente da errori
STRATO 1: strato fisico physical layer
Fornisce l’insieme dei collegamenti fisici fra i vari nodi su cui avviene la trasmissione dei dati in forma di successione di simboli binari.[:]


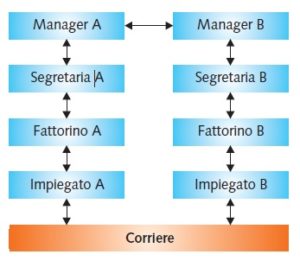



 Si richiede un certo tempo per la connessione fisica tra il nodo A alla linea C, poi un tempo di propagazione (che dipende dalla lunghezza della linea) e in maniera analoga tra il nodo C ed il nodo B.
Si richiede un certo tempo per la connessione fisica tra il nodo A alla linea C, poi un tempo di propagazione (che dipende dalla lunghezza della linea) e in maniera analoga tra il nodo C ed il nodo B.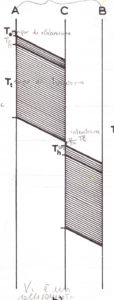
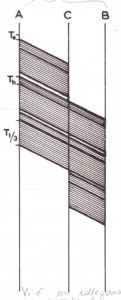 Il tempo di connessione sarà:
Il tempo di connessione sarà: