[:it]

jacek yerka
La telematica è la fusione di TELEcomunicazione e inforMATICA; essa, per poter funzionare ha la necessità che esista una rete, cioè un insieme di sistemi per l’elaborazione messi in comunicazione fra loro.
STORIA
Inizialmente esisteva il mainframe e dei semplici terminali che si connettevano con il mainframe con dei semplici cavi coassiali, nel momento in cui uno di essi veniva staccato dalla rete, solo il terminale in questione non poteva più comunicare senza inficiare il funzionamento del resto della rete.
Il disco fisso era presente solo sul calcolatore centrale.
Con l’abbassamento del costo dell’hardware si è passati al concetto moderno di rete in cui ogni PC è:
- autonomo: se disconnesso dalla rete esso può funzionare egregiamente
- interconnesso: scambia informazione con altri PC della rete
Una rete è un insieme di sistemi per l’elaborazione messi in comunicazione tra loro.
Si è passati quindi da sistemi di elaborazione delle informazioni aventi la caratteristica di essere concentrati, cioè strutture hardware composte da una singola CPU alla quale venivano connessi più terminali, alle stazioni di lavoro connesse tra loro e dotate di capacità elaborativa propria, cioè a sistemi distribuiti.
Nello stesso periodo la rete telefonica, in continuo sviluppo da quasi un secolo, ha subito una drastica ristrutturazione, concretizzandosi nella conversione delle centrali di commutazione da elettromeccaniche ad elettroniche e soprattutto nel passaggio, nei collegamenti fra le centrali di commutazione, da metodi di trasmissione analogica a metodi di trasmissione numerica.
Quindi si è passati dal MODEM all’ADSL di casa.
I MODEM modulano e demodulano il segnale ossia convertono il flusso di dati in un segnale analogico, con al conversione inversa in ricezione.
ADSL è acronimo di Asymmetric Digital Subscriber Line che consente la trasmissione, sempre su doppino telefonico di segnali solo digitali.
Il doppino telefonico in rame era stato progettato, e viene tuttora usato, per la comunicazione in voce, che utilizza frequenze tra 300 e 3.400 hertz.
Nel 1960 comincia a diffondersi la tecnica di trasmissione numerica, nota come PCM (Pulse Code Modulation), in cui la trasmissione di un segnale vocale è affidata ad un flusso di informazione di 64kbit/s. Più conversioni telefoniche sono poi affasciate mediante multiplazione a divisione di tempo (TDM Time Division Multiplexing) e trasmette su canali numerici con capacità dell’ordine dei Mbit/s.
Il grande boom delle reti è avvenuto grazie al Dipartimento della Difesa degli Stati Uniti, che ha svilupato ARPANET (Advanced Resercg Project Agency Net-work) che è riuscito a collegare macchine diverse con i più diversi sistemi operativi e potenze di calcolo diverse.
Per quest’ultimo problema è stata fondamentale l’attività degli organismi di standardizzazione che ha permesso di creare regole di comunicazione.[:]






 Il bit 1 controlla la parità dei bit 1, 3, 5, 7
Il bit 1 controlla la parità dei bit 1, 3, 5, 7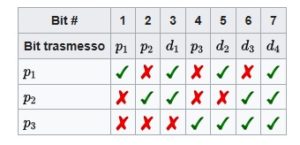 Si nota che:
Si nota che:


