[:it]

Vladimir Kush
L’informazione, nell’ambito delle telecomunicazioni, viene definita come la riduzione di incertezza che si poteva avere a priori sul simbolo trasmesso.
Sembra un panegirico ma, in realtà, il concetto è che se io trasmetto sempre un solo segnale sempre uguale, la probabilità di riceverlo è sempre 1. Ma tale fatto significa anche che l’informazione trasmessa è nulla.
Per trasmettere un’informazione vi è bisogno che si modifichi uno stato da luce a buio o viceversa; si pensi ai solo caratteri morse: per comunicare un messaggio, ossia un’informazione, si alternano i punti con le linee in un’opportuna combinazione.
Per dare una definizione che possa essere misurabile si utilizza la funzione logaritmo perché è l’unica che quando il suo argomento vale 1, il suo valore va a zero ed inoltre lo si caperà ancora di più quando si definisce l’entropia.
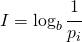
dove con 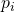 si intende la probabilità con cui quel simbolo possa presentarsi.
si intende la probabilità con cui quel simbolo possa presentarsi.
Se la base del logaritmo è:
- 2 l’informazione si misura in bit
- 10 l’informazione si misura in hartley
- e (numero di Eulero) l’informazione si misura in nat
[:en]trasmesso e viene definita come la riduzione di incertezza che si poteva avere a priori sul simbolo trasmesso.
Sembra un panegirico ma, in realtà, il concetto è che se io trasmetto sempre un solo segnale sempre uguale, la probabilità di riceverlo è sempre 1. Ma tale fatto significa anche che l’informazione trasmessa è nulla.
Per trasmettere un’informazione vi è bisogno che si modifichi uno stato da luce a buio o viceversa; si pensi ai solo caratteri morse: per comunicare un messaggio, ossia un’informazione, si alternano i punti con le linee in un’opportuna combinazione.
Per dare una definizione che possa essere misurabile si utilizza la funzione logaritmo perché è l’unica che quando il suo argomento vale 1, il suo valore va a zero ed inoltre lo si caperà ancora di più quando si definisce l’entropia.
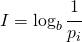
dove con 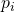 si intende la probabilità con cui quel simbolo possa presentarsi.
si intende la probabilità con cui quel simbolo possa presentarsi.
Se la base del logaritmo è:
2 l’informazione si misura in bit
10 l’informazione si misura in hartley
e (numero di Eulero) l’informazione si misura in nat[:de]trasmesso e viene definita come la riduzione di incertezza che si poteva avere a priori sul simbolo trasmesso.
Sembra un panegirico ma, in realtà, il concetto è che se io trasmetto sempre un solo segnale sempre uguale, la probabilità di riceverlo è sempre 1. Ma tale fatto significa anche che l’informazione trasmessa è nulla.
Per trasmettere un’informazione vi è bisogno che si modifichi uno stato da luce a buio o viceversa; si pensi ai solo caratteri morse: per comunicare un messaggio, ossia un’informazione, si alternano i punti con le linee in un’opportuna combinazione.
Per dare una definizione che possa essere misurabile si utilizza la funzione logaritmo perché è l’unica che quando il suo argomento vale 1, il suo valore va a zero ed inoltre lo si caperà ancora di più quando si definisce l’entropia.
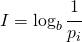
dove con 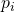 si intende la probabilità con cui quel simbolo possa presentarsi.
si intende la probabilità con cui quel simbolo possa presentarsi.
Se la base del logaritmo è:
2 l’informazione si misura in bit
10 l’informazione si misura in hartley
e (numero di Eulero) l’informazione si misura in nat[:]

![Rendered by QuickLaTeX.com \left [H=2,23\cfrac{bit}{sym} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-665b0fecaf5cb9cccdfbc8bfef9dea27_l3.png)
![Rendered by QuickLaTeX.com \left [ \gamma =0,07\cfrac{bit}{sym} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-38ba34b4187473c8be1b4b7f5e72ccf9_l3.png)
![Rendered by QuickLaTeX.com \left [ L=2,32,\gamma =0,1\cfrac{bit}{sym} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6981a76481622cb62d5ddbf0f33f03d5_l3.png)
![Rendered by QuickLaTeX.com \left [H =1,58\cfrac{bit}{sym}; \eta=0,6\cfrac{bit}{sym},L =2,581 ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-fb852f07b1c9060a910d2452e56b0fbb_l3.png)
![Rendered by QuickLaTeX.com \left [ H=1,922\cfrac{bit}{sym},I_{M_{1}}=7,528bit ,I_{M_{2}}=7,764bit \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b4ea083ecba402b061cf565bb47f0bec_l3.png)
![Rendered by QuickLaTeX.com \left [ H=1,548 \cfrac{bit}{sym},T_{s}=62,5\mu s, R=16\frac{kbit}{s} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b94d970a3ab06b0a8f86f17d5d7e1ec0_l3.png)

 Anno2015
Anno2015


![Rendered by QuickLaTeX.com \left [\cfrac{1}{36},\cfrac{1}{18},\cfrac{1}{4}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a7e343e044e002bf895dce4e19b0f2f0_l3.png)
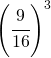 ;
;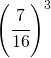 ;
;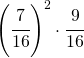 ;
;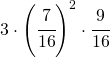



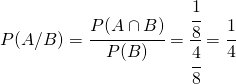 [:]
[:]