[:it]

Joan Miró
Credere di esaurire la teoria della probabilità in pochi post è un’impresa molto ardua, per cui esso si pone solo come punto di sviluppo per una trattazione più approfondita attraverso lezioni di approfondimento in aula o su libri strettamente specifici.
Il concetto di fenomeno aleatorio si contrappone a quello di fenomeno deterministico. Ad esempio il moto di un corpo sottoposto alla forza di gravità terrestre; le leggi della dinamica e della cinematica consentono di determinarne in modo esatto la traiettoria, note che siano le condizioni iniziali e il valore dell’accelerazione di gravità.
Note cioè le cause, si possono esattamente valutare gli effetti e il fenomeno si può considerare deterministico.
Da un’analisi più accurata si nota che le condizioni iniziali e l’accelerazione di gravità non sono mi esattamente note per le inevitabili incertezze di misura, la stessa traiettoria può essere osservata soltanto entro certi limiti d’approssimazione.
In queste circostanze la traiettoria del corpo non è esattamente prevedibile e il modello deterministico precedentemente considerato può fornire soltanto indicazioni di massima su quello che sarà la traiettoria osservata.
Può accadere tuttavia che un’analisi più accurata dei risultati riveli una sorta di REGOLARITA’ STATISTICA nel senso che la traiettoria “media” da definirsi in maniera opportuna, tende sempre più a stabilizzarsi con l’aumentare del numero di osservazioni.
Quest’ultima frase è alla base delle telecomunicazioni nel senso che un segnale trasmesso non si ha mai la certezza di come esso possa arrivare al destinatario ma si può descrivere in maniera statistico come esso possa arrivare al destinatario stesso e sapendo la funzione statistica che lo descrive si può prevedere come esso possa essere ricevuto.

Andrej Nikolaevič Kolmogorov
ASSIOMI DI KOLMOGROV
1- Ad ogni evento casuale a corrisponde un certo numero P(a), chiamato “probabilità di a“, che soddisfa la disuguaglianza ![]() .
.
2- La probabilità dell’evento certo è 1
3- La probabilità dell’unione di un numero finito o infinito numerabile di eventi mutuamente esclusivi è pari alla somma delle probabilità di questi eventi
La prima definizione porta quindi a definire la
![]()
dove m sono i casi favorevoli, ed n i casi possibili.[:]






 [:]
[:]

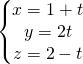
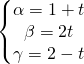
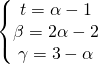
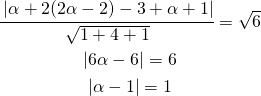
 [:]
[:]

 [:]
[:]