[:it]

Alex Alemany
Si immagini di trovarsi in questa situazione
La vincita del campionato delle seguenti squadre viene data seguendo la seguente tabella:
| Milan |
1:5 |
| Inter |
1:7 |
| Juve |
1:3 |
ossia:
se una persona scommette 1€ sulla vittoria del campionato del Milan guadagnerà 5€,
se scommette 1€ sulla vittoria del campionato dell’Inter guadagnerà 7€,
se scommet 1€ sulla vittoria del campionato della Juve guadagnerà 3€.
Vi sono due soggetti in questa situazione
- lo scommettitore che deve conoscere la probabilità di vincita
- il bookmaker che accetta e fissa le scommesse e non deve perderci anzi guadagnarsi
Conoscere il meccanismo probabilistico è necessario per capire se vale la pena giocare (non convine mai, alla lunga si perde sempre) e se vale la pena fare il bookmaker senza andare in fallimento!
Il ragionamento da cui si deve partire è il seguente:
la probabilità che esca testa è 
la probabilità che esca croce è 
allora il bookmaker mette le seguenti quote
1: 2 se esce testa
1:2 se esce croce
in questa maniera però il bookmaker alla fine della giornata di scommesse non avrà guadagnato nulla perchè la somma della probabilità di vincere mi dà l’evento certo ossia l’1.
NOTARE
la probabilità che esca testa vale  se e solo se si ha un limite infinito di lanci!
se e solo se si ha un limite infinito di lanci!
Per aver la probabilità in un numero finito di lanci bisogna parlare di distribuzioni di probabilità.
Allora per garantire il guadagno il bookmaker fissa le seguenti quote:
1:1.6 se esce testa ossia se scommetto 1€ ne guadagnerò 1€ e 60 centesimi.
1:1.5 se esce croce ossia se scommetto 1€ ne guadagnerò 1€ e 50 centesimi.
Naturalmente un bookmaker cercherà di evitare di esplicitare in maniera troppo evidente il suo guadagno e lo scommettitore deve stare attento alle probabilità di vincita.
Per capire la vera probabilità degli eventi partendo dalla quote del bookmaker si devono eseguire i seguenti calcoli:
Probabilità che esca testa per il bookmaker–> ![Rendered by QuickLaTeX.com P[testa]=\cfrac{1}{1.6}=0,625](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f83b6e9b590a7d62169dc8adc90634e9_l3.png)
Probabilità che esca croce per il bookmaker –>![Rendered by QuickLaTeX.com P[croce]=\cfrac{1}{1.5}=0,6](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2d0f0c4dcd3f0eed3e8dd9d76f4e684b_l3.png)
Sommo le probabilità e noto che 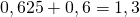 circa
circa
ossia il bookmaker ha la certezza di guadagnare!
Per capire la probabilità reale che esca testa si dovrà prendere la probabilità che esca testa per il bookmaker e dividerla per la probabilità complessiva del bookmaker (1,3).
Ossia:
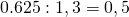
La probabilità che esca croce sarà
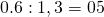
che già si sapevano nel caso del lancio delle monete.
Analizzando adesso il problema delle tre squadre di partenza il bookmaker ha garantito il suo guadagno? Qual è la probabilità che vinca il campionato, secondo le quote associate, la relativa squadra?[:]
![]()
![]()
![]() e
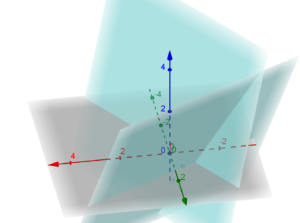
e ![]() sono uno combinazione lineare dell’altro.
sono uno combinazione lineare dell’altro.![]()
![]()
![]()
![]()
![]()
![]()
![]() e
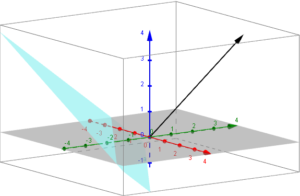
e ![]() è nullo.
è nullo.![]()
![]()
![]()
![]()
![]()
![]()

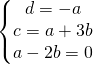
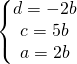



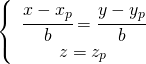
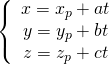
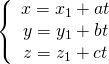

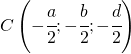

 [:]
[:]
