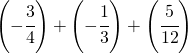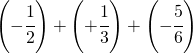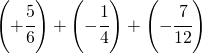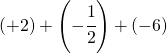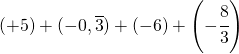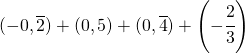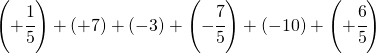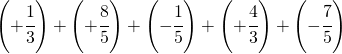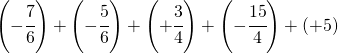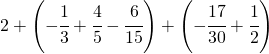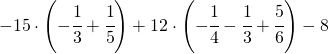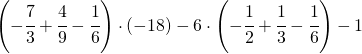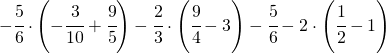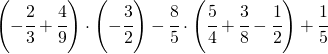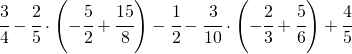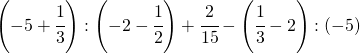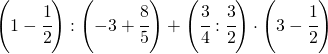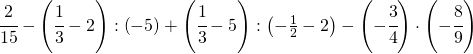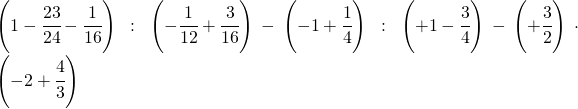[:it]

Claudio Souza Pinto
Sia P un punto di una semicirconferenza di diametro AB=2 e sia K il punto di AB per il quale AK=AP. Posto ![]() , esprimi, in funzione di x, il rapporto fra l’area del cerchio inscritto nel triangolo APB e l’area del triangolo APK. Indicata con
, esprimi, in funzione di x, il rapporto fra l’area del cerchio inscritto nel triangolo APB e l’area del triangolo APK. Indicata con ![]() la funzione che esprime tale rapporto:
la funzione che esprime tale rapporto:
- determina il suo comportamento per P che tende ad A e a B e stabilisci se la funzione è continua rispettivamente a destra di A e a sinistra di B.
- determina il suo dominio indipendentemente dalle limitazioni imposte dal problema e stabilisci se la funzione possiede asintoti.
- studiare il segno e costruisci un probabile grafico.
PREREQUISITI
- conoscere come determinare il raggio della circonferenza inscritta in un triangolo rettangolo
- le relazioni fondamentali tra il lato e l’angolo opposto od adiacente di un triangolo rettangolo
- saper calcolare i limiti
- conoscere le formule parametriche per il seno ed il coseno
- conoscere la definizione di asintoto
- saper tracciare un grafico di una funzione ed il relativo segno
SVILUPPO
Si ha la seguente situazione grafica:
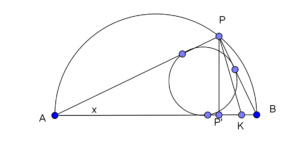
Area del cerchio inscritto nel triangolo APB.
Si utilizza la seguente relazione che lega il raggio alle lunghezze dei lati del triangolo rettangolo.
![]()
(1) ![]()
![]()
![]()
![]()
ossia
![]()
Area del cerchio inscritto risulta:
(2) ![]()
Area del triangolo APK
AK=AP per ipotesi e già precedentemente trovata (1)
![]()
![]()
![]()
ossia:
(3) ![]()
Si ha la funzione cercata effettuando il rapporto tra la (2) e la (3)
(4) ![]()
la (4) si può opportunamente manipolare per non avere un situazione di indeterminatezza quando l’angolo varia dal valore nullo a 90°.
Si moltiplica il numeratore ed il denominatore per:
![]()
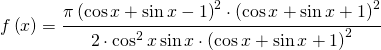
Si ha il quadrato della differenza di un binomio
![Rendered by QuickLaTeX.com f\left ( x \right )=\cfrac{\pi \left [\left ( \cos x+\sin x-1 \right ) \cdot \left ( \cos x+\sin x+1 \right ) \right ]^{2} }{2\cdot \cos^{2} x\sin x\cdot \left ( \cos x+\sin x+1 \right )^{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc8c5cb6037c7ed0442025322fdcacdb_l3.png)
![Rendered by QuickLaTeX.com f\left ( x \right )= \cfrac{\pi \left [\left ( \cos x+\sin x \right )^{2}-1 \right ]^{2} }{2\cdot \cos^{2} x\sin x\cdot \left ( \cos x+\sin x+1 \right )^{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e63f981fbcc64f0fe0127326b9912d90_l3.png)
![Rendered by QuickLaTeX.com f\left ( x \right )= \cfrac{\pi \left [ \cos^{2} x+\sin^{2} x +2\cdot \sin x\cdot \cos x-1 \right ]^{2} }{2\cdot \cos^{2} x\sin x\cdot \left ( \cos x+\sin x+1 \right )^{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b36be750e891ae4f1a839cdfa6355785_l3.png)
ma ![]()
per cui:
![Rendered by QuickLaTeX.com f\left ( x \right )= \cfrac{\pi \left [ 1 +2\cdot \sin x\cdot \cos x-1 \right ]^{2} }{2\cdot \cos^{2} x\sin x\cdot \left ( \cos x+\sin x+1 \right )^{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5d0d5fffc1aa00f5f0d82bda5b255c54_l3.png)
![Rendered by QuickLaTeX.com f\left ( x \right )= \cfrac{\pi \left [ \not 1 +2\cdot \sin x\cdot \cos x-\not 1 \right ]^{2} }{2\cdot \cos^{2} x\sin x\cdot \left ( \cos x+\sin x+1 \right )^{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5e671e2d41e9e0a370918e948c706d03_l3.png)
![Rendered by QuickLaTeX.com f\left ( x \right )= \cfrac{\pi \left [2\cdot \sin x\cdot \cos x \right ]^{2} }{2\cdot \cos^{2} x\sin x\cdot \left ( \cos x+\sin x+1 \right )^{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-eaea5edafe4b5925982f1c98a10b7e1b_l3.png)
![]()
semplificando opportunamente il numeratore con il denominatore la (4) diventa:
(5) ![]()
Adesso si può sviluppare il punto a.
Se il punto P si sposta verso A significa calcolare ![]()
Se il punto P si sposta verso B significa calcolare ![]()
Quindi calcolare il seguente limite
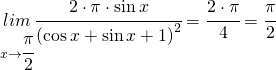
![]()
La funzione nei sui estremi non presenta discontinuità in quanto il valore del limite coincide con il valore della funzione in tali punti.
Per approfondire tale cosa il punto successivo lo rafforza.
Punto b
Adesso si studia la funzione (5) nei dettagli:
(5) ![]()
Si escludono dal dominio i valori che annullano il denominatore ossia bisogna risolvere l’equazione:
![]()
I valori che annullano il quadrato sono gli stessi che annullano:
![]()
Per studiare gli zeri dell’equazione:
(6) ![]()
uso le formule parametriche del seno e coseno ossia:
![]() e
e ![]() con
con
![]()
Siccome la tangente è definita ovunque tranne che per ![]()
bisogna verificare se tali valori risolvono la (6)
Sostituendo ![]() si ha:
si ha:
![]()
Si annulla per cui si hanno già dei valori da escludere dal dominio:
![]()
Adesso risolvo l’equazione parametrica:
![]()
facendo il minimo comune multiplo e togliendo il denominatore che non si annulla mai nel campo dei numeri reali mi ritrovo questa equazione:
![]()
che si riduce a:
![]()
![]()
che si annulla per
![]()
ossia
![]()
Ricapitolando il dominio di
(5) ![]()
è:
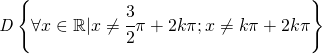
i valori che annullano il denominatore sono i punti che corrispondono agi asintoti verticali. Non vi sono asintoti orizzontali in quanto è indeterminato il limite per ![]() . Non vi sono nemmeno asintoti obliqui per lo stesso motivo precedente.
. Non vi sono nemmeno asintoti obliqui per lo stesso motivo precedente.
Punto c
Per studiare il segno è sufficiente studiare il segno del numeratore in quanto il denominatore è sempre positivo.
La funzione seno è sempre positiva per ![]() .
.
Il dominio lo si è già trovato per cui l’andamento della funzione è il seguente:
 [:]
[:]



 Quando unisco due punti creo un segmento, se questo viene prolungato ai suoi estremi creo una retta.
Quando unisco due punti creo un segmento, se questo viene prolungato ai suoi estremi creo una retta.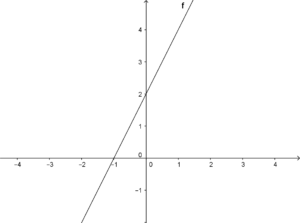 [:]
[:]

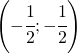 e B(1,1)
e B(1,1)
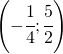
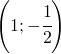
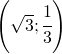

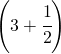 °C e poi cresce di 1,5 °C, infine discende di altri 4 °C. Che temperatura segna il termometro?
°C e poi cresce di 1,5 °C, infine discende di altri 4 °C. Che temperatura segna il termometro?
 Sommare numeri relativi frazionari dignifica applicare comunque tutto ciò che si è appreso con la somma delle frazioni.
Sommare numeri relativi frazionari dignifica applicare comunque tutto ciò che si è appreso con la somma delle frazioni.