[:it]

Norman Rockwell
Ricordiamoci che i numeri devono essere sempre pensati con il relativo segno.
Per sommare i numeri relativi:
SE DI SEGNO OPPOSTO:
- SI PRENDE IL NUMERO PIU’ GRANDE SENZA IL SEGNO E GLI SI SOTTRAE IL PIU’ PICCOLO
- AL NUMERO RISULTANTE SI METTE IL SEGNO DEL NUMERO PIU’ GRANDE
SE DI SEGNO UGUALE:
- SI SOMMANO I DUE NUMERI SENZA IL SEGNO
- AL NUMERO RISULTANTE SI METTE IL SEGNO DI PARTENZA
Esercizi di base.
Mettere al posto dei puntini il segno opportuno (< minore; > maggiore; = uguale)
| A.1. -14…+3 | |
| A.2. -15…+15 | |
| A.3. +10…-15 | |
| A.4. -19…+11 | |
| A.5. +3,5 …-26 | |
| A.6. |
|
| A.7. |
|
| A.8. |
Determinare, per ciascuna delle seguenti coppie di numeri relativi, qual è il minore:
| B.1. -5,+7 | |
| B.2. |
|
| B.3. |
|
| B.4. |
|
| B.5. |
Completa inserendo opportunamente i simboli > (maggiore), < (minore)
| C.1. |
|
| C.2. |
|
| C.3. |
|
| C.4. |
|
| C.5. |
|
| C.6. |
Facendo uso del simbolo < (minore), disporre in ordine crescente i numeri relativi di ciascuno dei seguenti gruppi. Inserire i numeri sull’asse dei nuemri relativi.
| D.1. -3; +3; +1; |
| D.2. +2; 0; |
[:]





 Trovare una soluzione non significa che si debba conoscere esattamente il suo valore preciso ma è sufficiente uno approssimato.
Trovare una soluzione non significa che si debba conoscere esattamente il suo valore preciso ma è sufficiente uno approssimato. Questo teorema garantisce che un’equazione vista come funzione possa avere una soluzione.
Questo teorema garantisce che un’equazione vista come funzione possa avere una soluzione. Studiare il grafico di una funzione non è cosa assolutamente semplice, inoltre spesso non interessa il grafico completo ma solo il suo andamento in un intorno di un suo determinato punto.
Studiare il grafico di una funzione non è cosa assolutamente semplice, inoltre spesso non interessa il grafico completo ma solo il suo andamento in un intorno di un suo determinato punto.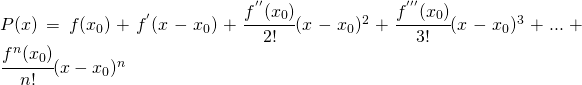

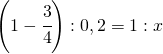
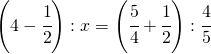
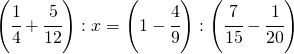
![Rendered by QuickLaTeX.com \left ( \cfrac{1}{3} +\cfrac{1}{2}\right )^{2}:\left ( 1-\cfrac{1}{6} \right )^{2}=x: \left [\left ( \cfrac{4}{7} \right )^{2} \cdot \left ( 2-\cfrac{1}{4} \right )^{2}+2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-06032fbf4196b354d5d3e767c782323c_l3.png)
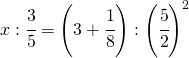
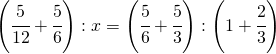
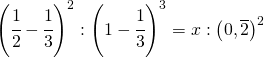
![Rendered by QuickLaTeX.com \left [ \left ( \cfrac{1}{6} \right )^{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-00f3619d672e11be36f3112e4bfd4a2f_l3.png)
![Rendered by QuickLaTeX.com x:\left [ \left ( \cfrac{3}{4}+\cfrac{5}{2} \right )^{2}:\left ( \cfrac{13}{4} \right )^{2} \right ]=\left [ \left ( 2\cdot \cfrac{3}{10} \right )^{2}:\left ( \cfrac{9}{4}-\cfrac{9}{5} \right )^{2} \right ]:x](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-732a717523a645b03a56f4f0e6130e22_l3.png)
