[:it]

Norman Rockwell
Questo metodo si usa quando la derivata seconda mantiene costante il suo segno nell’intervallo entro il quale vi è la soluzione.
Esso si basa sulla determinazione della derivata prima e quindi sulla determinazione della retta tangente nell’estremo la cui ordinata è concorde con la 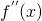 .
.
La tangente ad una curva in un punto si calcola:
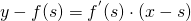
deve  è
è 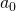 o
o 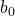 a seconda che
a seconda che 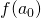 o
o 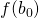 siano concordi, nell’intervallo, con
siano concordi, nell’intervallo, con 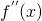 .
.
La soluzione è l’intersezione della retta tangente con l’asse delle ascisse per cui si ha:
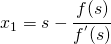
generalizzando, il procedimento è il seguente:
Il punto di partenza della successione approssimata è l’estremo dell’intervallo in cui la funzione ha lo stesso segno della derivata seconda.
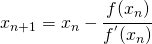
Ci si ferma nella reiterazione quando
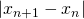 è minore della precisione richiesta.
è minore della precisione richiesta.
CONCLUSIONE SUI TRE METODI
Si arriva molto velocemente con il metodo delle tangenti ma esso richiede la conoscenza della derivata prima ed anche del segno della derivata seconda.
Con il primo metodo invece non si richiede alcuna derivata ma soltanto un procendimento molto meccanico.
[:]








 Trovare una soluzione non significa che si debba conoscere esattamente il suo valore preciso ma è sufficiente uno approssimato.
Trovare una soluzione non significa che si debba conoscere esattamente il suo valore preciso ma è sufficiente uno approssimato. Questo teorema garantisce che un’equazione vista come funzione possa avere una soluzione.
Questo teorema garantisce che un’equazione vista come funzione possa avere una soluzione. Studiare il grafico di una funzione non è cosa assolutamente semplice, inoltre spesso non interessa il grafico completo ma solo il suo andamento in un intorno di un suo determinato punto.
Studiare il grafico di una funzione non è cosa assolutamente semplice, inoltre spesso non interessa il grafico completo ma solo il suo andamento in un intorno di un suo determinato punto.