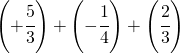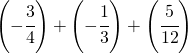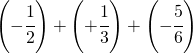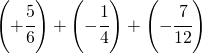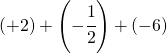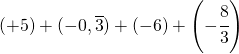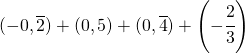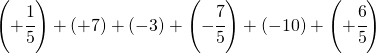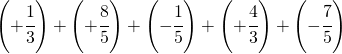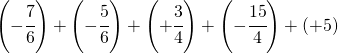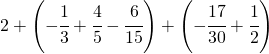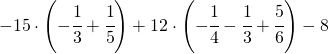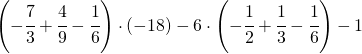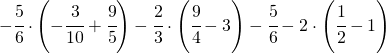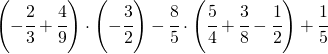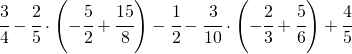SCIENZE E TECNOLOGIE INFORMATICHE

[:it]

Andreas Angelidakis

1. Su un corpo M sono applicate, nella stessa direzione AA’, le seguenti forze, positive nel senso da M ad A, negative nel senso opposto:

52Kg, 25Kg, -74Kg, 9 Kg, 15Kg, -103Kg

Dire qual è la risultante.

(Si ricordi dalla fisica che, in questo caso, la risultante, è data, per intensità, dalla somma algebrica dell’intensità delle forze componenti).

[-76Kg]

2. Quanti anni sono trascorsi dalla nascita di Aristotele, avvenuta nel 344 a.C., alla morte di Giulio Cesare avvenuta nel 44 a.C.? E a quella di Caligola, avvenuta nel 41 d.C.?

( Si indichino gli anni prima di Cristo con i numeri negativi e quelli dopo di Cristo con i numeri positivi)

[300;385]

3. In un grattacielo, un ascensore parte dal settimo piano e sale di nove piani, poi scende di cinque piani e quindi di altri dieci. Di quanti piani deve salire l’ascensore per giungere al tredicesimo piano?

[12]

4. Un automobilista percorre 20 Km su una stessa strada, poi altri 45 nel verso opposto, quindi 42 nel verso iniziale, ed infine altri 17 nel verso opposto. Qual è stata la distanza massima dal punto di partenza che l’automobilista ha raggiunto? A che punto i trova ora?

[25Km; al punto di partenza]

5. Un tale preleva dal suo conto corrente 350€, il giorno dopo versa 200€ e successivamente preleva 70€. L’ammontare del suo credito è così di 10.000€. Qual era il suo credito prima di queste operazioni?

[10.220€]

6. Un punto P, mobile sopra una retta, percorre, a partire da un punto A, in n certo verso, poi 6,5m nel verso opposto, quindi 3,2m nel verso iniziale. A che distanza da A si trova P?

[2,9m]

5. Un termometro segna 16°C sopra lo zero, la temperatura si abbassa di 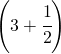°C e poi cresce di 1,5 °C, infine discende di altri 4 °C. Che temperatura segna il termometro?

[9,75 °C]

7. Uno scalatore parte da un campeggio posto a 1100 m sul livello del mare; sale per 500m, discende per 110m, risale per 971m e discende per 75m. A quale altezza, sul livello del mare, si troverà alla fine?

[+2386m]

[:]

[:it]

Paul David bond

[WpProQuiz 41]

[:]

[:it]Sommare numeri relativi frazionari dignifica applicare comunque tutto ciò che si è appreso con la somma delle frazioni.

Lo richiamo qui con un esempio perché tutta la teoria è presente nel post:

somma tra frazioni

Allora:

Esercizi suddivisi per un livello sufficiente [6]:

6.1.   (+3)+(-5)+(-6)	[-8]
6.2. (+8) + (-10)+(+11)	[+9]
6.3. (-1)+(-3)+(-7)	[-11]
6.4. (-2)+(+7)+(-8)	[-3]
6.5.
6.6.
6.7.	[ -1 ]
6.8.	[ 0]
6.9.
6.10.
6.11.
6.12.	[-6]
6.13.
6.14.	[0]
6.15. (+13)+(+32)+(-5)+(-7)+(-10)+(+7)	[+30]
6.16. (-25)+(-10)+(+8)+(+2)+(+4)+(+13)	[-8]
6.17. (15-9)+(11+4-28-9)+(-8+16-11)	[-19]
6.18.	[+2]

Si devono eseguire le operazioni a partire da quelle contenute nelle parentesi più interne

Esercizi per un livello discreto [7]:

7.1.	[-3]
7.2.	[+38]
7.3.
7.4.
7.5.

Esercizi per un buon livello [8]

8.1.
8.2.
8.3.	[+1]

Esercizi per un ottimo livello [9/10]

10.1.

Soluzioni guidate agli esercizi[:]

[:it]

Norman Rockwell

Questo esercizio richiede:

• utilizzo completamento automatico
• utilizzare il simbolo somma
• collegare il valore presente in un foglio con il valore presente in un altro foglio
• inserire un istogramma /grafico
• inserire un grafico a torta
• modificare i colori degli istogrammi

Modulo4esercizio2[:]

[:it]

Norman Rockwell

In questo primo esercizio si deve sapere:

• identificare le celle attraverso le sue coordinate
• unire celle diverse
• sostiutire il contenuto di una cella
• aumentare o diminuire il numero di decimali
• inserire la formula che fornisce la media
• rinominare un foglio

modulo4esercizio[:]

[:it]

Norman Rockwell

Ricordiamoci che i numeri devono essere sempre pensati con il relativo segno.

Per sommare i numeri relativi:

SE DI SEGNO OPPOSTO:

• SI PRENDE IL NUMERO PIU’ GRANDE SENZA IL SEGNO E GLI SI SOTTRAE IL PIU’ PICCOLO
• AL NUMERO RISULTANTE SI METTE IL SEGNO DEL NUMERO PIU’ GRANDE

SE DI SEGNO UGUALE:

• SI SOMMANO I DUE NUMERI SENZA IL SEGNO
• AL NUMERO RISULTANTE SI METTE IL SEGNO DI PARTENZA

Esercizi di base.

Mettere al posto dei puntini il segno opportuno (< minore; > maggiore; = uguale)

A.1. -14…+3
A.2. -15…+15
A.3. +10…-15
A.4. -19…+11
A.5. +3,5 …-26
A.6.
A.7.
A.8.

Determinare, per ciascuna delle seguenti coppie di numeri relativi, qual è il minore:

B.1. -5,+7
B.2.
B.3.
B.4.
B.5.

Completa inserendo opportunamente i simboli > (maggiore), < (minore)

C.1.
C.2.
C.3.
C.4.
C.5.
C.6.

Facendo uso del simbolo < (minore), disporre in ordine crescente i numeri relativi di ciascuno dei seguenti gruppi. Inserire i numeri sull’asse dei nuemri relativi.

D.1. -3; +3; +1; ;

D.2. +2; 0; ; ; ; -4; -1,3; +11,6; -5,4;

[:]

[:it]

Jack Vettriano

[WpProQuiz 40]

[:]

[:it]

Norman Rockwell

Questo metodo si usa quando la derivata seconda mantiene costante il suo segno nell’intervallo entro il quale vi è la soluzione.

Esso si basa sulla determinazione della derivata prima e quindi sulla determinazione della retta tangente nell’estremo la cui ordinata è concorde con la .

La tangente ad una curva in un punto si calcola:

deve è o a seconda che o siano concordi, nell’intervallo, con .

La soluzione è l’intersezione della retta tangente con l’asse delle ascisse per cui si ha:

generalizzando, il procedimento è il seguente:

Il punto di partenza della successione approssimata è l’estremo dell’intervallo in cui la funzione ha lo stesso segno della derivata seconda.

Ci si ferma nella reiterazione quando

è minore della precisione richiesta.

CONCLUSIONE SUI TRE METODI

Si arriva molto velocemente con il metodo delle tangenti ma esso richiede la conoscenza della derivata prima ed anche del segno della derivata seconda.

Con il primo metodo invece non si richiede alcuna derivata ma soltanto un procendimento molto meccanico.

 [:]

[:it]

Norman Rockwell

Per trovare la soluzione in questo caso, invece che trovare il punto medio, come nel metodo di bisezione, si trova la retta passante per i due punti, per cui vale il teorema di unicità della radice, e si determina il suo punto di intersezione con l’asse delle x.

L’errore o approssimazione è data dalla differenza tra le due intersezioni successive ossia:

La retta passante per i due estremi ha equazione:

e la sua intersezione vale:

Ecco il metodo ricorsivo per determinare la soluzione:

Data l’equazione , si cerchi un intervallo tale che .

1. Calcolare
2. Calcolare
3. Se allora è proprio la soluzione e si termina il ciclo altrimenti si va al passo successivo.
4. Solo al passo successivo al primo si calcola , se risulta minore della precisione voluta, si termina il ciclo uscendo.
5. Se si deve scegliere il nuovo intervallo con il seguente criterio:

se allora ,

se allora ,

6. Si torna al punto 1 con i nuovi intervalli.

Nel caso in cui il segno della derivata seconda mantenesse lo stesso segno (ossia la curva mantenesse la stessa concavità) nell’intervallo trovato, il procedimento si semplifica notevolmente e si ha la seguente ricorsione.

Se

allora

Se

allora

 [:]

[:it]

Norman Rockwell

Questo mio approfondimento nasce dall’esigenza di chiarire quando due funzioni logaritmiche sono uguali o meno.

In particolare è corretto affermare che:

?

Se applicassimo la proprietà dei logaritmi senza alcuna riflessione in merito la risposta sarebbe affermativa.

Se andiamo ad effettuare il grafico delle due funzioni ci si accorge che sono uguali solo per .

Allora dove sta la soluzione al problema?

Per applicare la proprietà bisogna prima studiare il dominio ossia scrivere la relazione precedente è possibile farlo solo dopo aver evidenziato che si può fare solo e soltanto per .

Se si fosse richiesto invece di studiare solo la funzione:

allora il dominio sarebbe stato tutto esclusa l’origine.[:]