[:it]

Paul David Bond
Spesso, da una tabella si richiedono dei raggruppamenti, sapere la somma di colonne numeriche, sapere quante colonne fanno parte di una tabella.
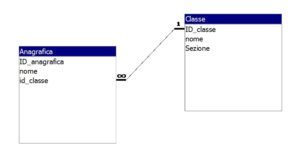
Ad esempio riprendendo l’esempio degli alunni di una classe del post Join, si vuole sapere quanti sono gli alunni di una classe.
COMANDO GROUP BY e COUNT(*)
Bisogna raggrupparli per classe e contare quanti sono.
In una scuola vi sono molti alunni e molte classi per cui il conto manuale sarebbe improponibile e fonte di numerosi errori.
Il comando per sapere quanti sono gli alunni di una classe risulta il seguente:
SELECT
count(*)
FROM
anagrafica
GROUP By id_classe
L’esito della query precedente fornisce il seguente risultato:
Come si nota una query del genere ha poco significato ed è di difficile lettura allora voglio anche il nome della classe di cui si vuole conoscere il numero degli studenti.
La query, indubbiamente complessa è la seguente:
SELECT
classe.nome,
count(*)
FROM
anagrafica,
classe
WHERE
anagrafica.id_classe=classe.id_classe
GROUP BY anagrafica.id_classe, classe.nome;
Riflessioni su questa query:
all’interno del comando Group by si deve mettere sia l’id_classe che il nome della classe ossia le stesse colonne che compaiono nella SELECT.
L’esito è il seguente:
group by
| nome |
Expr1001 |
| Prima |
4 |
| Seconda |
3 |
Adesso l’esito è indubbiamente migliore ma non ancora il massimo!
Il nome delle colonne non è chiarissimo ma voglio dare un nome più coerente con il suo contenuto.
AS
Il comando AS permette di rinominare una colonna.
Nel caso della query precedente si ha:
SELECT
classe.nome AS classe,
Count(*) AS studenti
FROM
anagrafica,
classe
WHERE
anagrafica.id_classe=classe.id_classe
GROUP BY classe.nome, anagrafica.id_classe;
SUM
Supponiamo adesso che ogni studente abbia versato una quota per la partecipazione della gita e voglio sapere il totale della cifra a disposizione.
Naturalmente la tabella Anagrafica deve contemplare adesso la colonna quota all’interno della quale si è inserita la cifra versata dal relativo studente.
La tabella anagrafica contiene i seguenti dati:
selectanagrafica
| ID_anagrafica |
nome |
id_classe |
quota |
| 1 |
Paolo |
1 |
€ 41,00 |
| 2 |
Filippo |
1 |
€ 32,00 |
| 3 |
Maria |
1 |
€ 25,00 |
| 4 |
Giovanna |
1 |
€ 32,00 |
| 5 |
Tommaso |
2 |
€ 52,00 |
| 6 |
Marta |
2 |
€ 12,00 |
| 7 |
Giovanna |
2 |
€ 12,00 |
La query sarà la seguente:
SELECT
SUM(quota) AS TOTALE
from anagrafica
WHERE
id_classe=1;
che fornisce come risultato:
AVG
Se voglio conoscere il valore medio della quota versata dai singoli ragazzi si deve eseguire la seguente query.
SELECT
AVG(quota) AS media
from anagrafica
WHERE
id_classe=1;
che fornisce come risultato:
[:]