[:it]Un database relazionale come Access sono in genere diverse tabelle correlate. In un database ben progettato ogni tabella vengono memorizzati dati relativi a un argomento specifico, ad esempio dipendenti o dei prodotti. Una tabella con i record (righe) e campi (colonne).
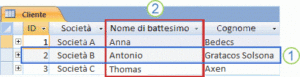
- Un record: contiene dati specifici, ad esempio informazioni su un determinato dipendente o un prodotto.
- Un campo: contiene i dati relativi a un aspetto dell’oggetto tabella, ad esempio nome o indirizzo di posta elettronica.
- Un valore di campo: ogni record è un valore di campo. Ad esempio, Contoso, Ltd.
Durante la creazione di tabelle in Access, è necessario selezionare un tipo di dati per ogni colonna di dati. Il tipo di dati testo breve è una scelta popolare perché consente di immettere quasi tutti i caratteri (lettere, simbolo o numero). Tuttavia, accurata selezione dei tipi di dati consentono di sfruttare altre caratteristiche di accesso (ad esempio la convalida dei dati e funzioni) e migliora la precisione delle informazioni è archiviato.
| Tipo di dati |
Utilizzo |
|
| Testo breve (in precedenza noto come “Testo”) |
Dati alfanumerici (nomi, titoli e così via) |
|
| Testo lungo (in precedenza noto come “Memo”) |
Grandi quantità di dati alfanumerici: frasi e paragrafi. |
|
| Numero |
Dati numerici. |
|
| Data/ora |
Date e ore. |
|
| Valuta |
Dati monetari, archiviati con una precisione di 4 posizioni decimali. |
|
| Numerazione automatica |
Valori univoci generati da Access per ogni nuovo record. |
|
| Sì/No |
Dati booleani (vero/falso). Access archivia il valore numerico zero (0) per falso e -1 per vero. |
|
| Oggetto OLE |
Immagini, grafici o altri oggetti ActiveX di altre applicazioni basate su Windows. |
|
| Collegamento ipertestuale |
Indirizzo di un collegamento a un documento o un file su Internet, in una rete Intranet, in una rete locale (LAN) o sul computer locale |
|
| Allegato |
È possibile allegare file come immagini, documenti, fogli di calcolo o grafici. Ogni campo Allegato può contenere un numero illimitato di allegati per ogni record, fino al limite di archiviazione della dimensione di un file di database. |
|
| Valore calcolato |
È possibile creare un’espressione che utilizza dati da uno o più campi e designare diversi tipi di dati per i risultati dell’espressione. |
|
| Ricerca guidata |
La voce Ricerca guidata nella colonna Tipo di dati in visualizzazione Struttura non è un vero e proprio tipo di dati. Quando si sceglie questa voce, viene avviata una procedura guidata che consente di definire un campo di ricerca semplice o complesso. Un campo di ricerca semplice utilizza il contenuto di un’altra tabella o un elenco di valori per convalidare il contenuto di un singolo valore per ogni riga. Un campo di ricerca complesso consente di archiviare più valori dello stesso tipo di dati in ogni riga. |
|
Le caratteristiche e il comportamento di tabelle e campi sono definiti e controllate dalle proprietà. Proprietà della tabella sono impostate nella finestra delle proprietà della tabella, ad esempio, è possibile impostare proprietà di visualizzazione predefinita di una tabella per specificare la modalità di visualizzazione della tabella per impostazione predefinita. Proprietà del campo definisce un aspetto del comportamento del campo. Per impostare le proprietà dei campi in visualizzazione struttura utilizzando il riquadro di proprietà dei campi. Tutti i campi di tipo di dati che definisce il tipo di informazioni memorizzate nel campo. Ad esempio, più righe di testo o valuta sono i tipi di dati.
Dopo aver creato o modificato una tabella, è consigliabile salvare la struttura in un database desktop. Quando si salva una tabella per la prima volta, assegnare un nome che descriva i dati che contiene. Ad esempio, si potrebbe assegnare un nome a una tabella clienti, inventario delle parti o prodotti.
È possibile utilizzare un indice per consentire ad Access di trovare e ordinare i record più velocemente. La posizione dei record viene memorizzata in base al campo o ai campi inclusi nell’indice. A seconda del numero di valori univoci dei campi indicizzati, le dimensioni di un indice possono risultare inferiori alla tabella in esso descritta, rendendone più efficiente la lettura da parte di Access.
Quando si assegna un nome a un campo, un controllo o un oggetto, è consigliabile assicurarsi che il nome non duplichi quello di una proprietà di un altro elemento utilizzato, in quanto potrebbe produrre risultati imprevisti. Se si fa riferimento ad esempio al valore di un campo Nome elemento in una tabella InfoSulNome utilizzando la sintassi InfoSulNome.NomeElemento, viene visualizzato il valore della proprietà Nome della tabella e non il valore del campo Nome.
È possibile impostare proprietà valide per un’intera tabella o per interi record.
Quando si crea una nuova tabella o si apre una tabella esistente in visualizzazione Foglio dati, è possibile aggiungervi subito un campo immettendo i dati desiderati nella colonna Aggiungi nuovo campo del foglio dati.
In visualizzazione Foglio dati è possibile rinominare un campo, modificarne il tipo di dati, impostare la proprietà Formato e modificare alcune altre proprietà dei campi.
Nomi dei campi, controlli e oggetti in database desktop di Microsoft Access:
- Possono contenere fino a 64 caratteri.
- Possono contenere qualsiasi combinazione di lettere, numeri, spazi e caratteri speciali, a eccezione del punto (.), del punto esclamativo (!), dell’accento grave (`) e delle parentesi quadre ([]).
- Non possono avere spazi iniziali.
- Non possono contenere caratteri di controllo, cioè valori ASCII da 0 a 31.
- Non possono contenere virgolette doppie (“) nei nomi di tabelle, viste o stored procedure di un progetto di Microsoft Access.
Dopo aver creato un campo, è possibile impostarne le proprietà per definire aspetto e comportamento.
L’impostazione delle proprietà dei campi consente ad esempio di:
- Stabilire l’aspetto dei dati in un campo
- Impedire l’immissione di dati errati in un campo
- Specificare valori predefiniti per un campo
- Velocizzare le operazioni di ricerca e ordinamento
Alcune delle proprietà disponibili per i campi possono essere impostate nella visualizzazione Foglio dati. Per accedere all’elenco completo delle proprietà che è possibile impostare, è tuttavia necessario utilizzare la visualizzazione Struttura.
NOTE:
- Nel calcolo non possono essere inclusi campi da altre tabelle o query.
- I risultati del calcolo sono di sola lettura.
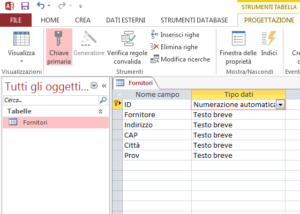
Una chiave primaria è un campo o un set di campi con valori univoci all’interno di una tabella. È possibile utilizzare i valori della chiave per fare riferimento a interi record poiché il valore della chiave è diverso per ogni record. Ogni tabella può includere una sola chiave primaria.
Per impostare la chiave primaria di una tabella, aprire la tabella nella visualizzazione Struttura. Selezionare il campo o i campi da utilizzare e quindi sulla barra multifunzione fare clic su Chiave primaria.
In Access i campi chiave primaria vengono utilizzati per diversi scopi:
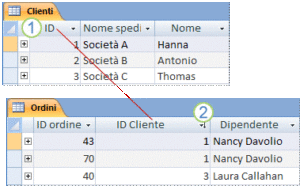
- Per leggere dati di diverse tabelle e combinarli in modo significativo. È possibile includere i campi chiave primaria in altre tabelle per fare riferimento alla tabella che corrisponde all’origine della chiave primaria. In queste altre tabelle i campi sono denominati chiavi esterne. Un campo ID cliente nella tabella Clienti ad esempio potrebbe essere visualizzato anche nella tabella Ordini. Nella tabella Clienti tale campo corrisponde alla chiave primaria, mentre nella tabella Ordini è denominato chiave esterna. In termini semplici, una chiave esterna è la chiave primaria di un’altra tabella.
I tipi di valori più adatti a costituire la chiave primaria sono contraddistinti da diverse caratteristiche:
- Devono identificare ogni riga in modo univoco.
- Non devono essere mai vuoti o Null, ovvero devono sempre contenere un valore.
- Non devono essere mai, se non molto raramente, modificati.
Se non si riesce a identificare una chiave appropriata, creare un campo Numerazione automatica da utilizzare come chiave, che genera automaticamente un valore quando si salva un record per la prima volta.

Un campo Numerazione automatica costituisce una chiave primaria appropriata.[:]
.