[:it]
Relazioni tra tabelle
Le relazioni tra tabelle normalmente si basano sulla chiave primaria di una delle tabelle. La chiave primaria è un identificatore univoco (spesso numerico) per ogni record. Per mostrare che le informazioni contenute in due tabelle diverse sono correlate, in genere si crea una relazione usando la chiave primaria di una delle tabelle.
Perché organizzare e relazionare i dati in tabelle?
- Gestione di una grossa mole di dati
- Evitare duplicazioni
- Controllare aggiunte e cancellazioni
- Ottimizzare l’accesso alle informazioni
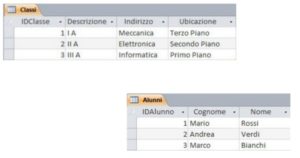
Vogliamo indicare che tutti gli alunni appartengono alla stessa classe, la III A Informatica.
Soluzione ERRATA: Aggiungiamo i campi della tabella Classi alla tabella Alunni e ricopiamo i dati del record III A Informatica:
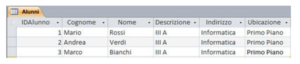
Problema 1: otteniamo una gran quantità di dati ripetuti che aumentano notevolmente la dimensione del database.
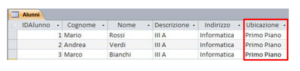
Problema 2: se la classe III A subisce uno spostamento di piano devo riorganizzare tutti i record correlati (sia nella tabella Alunni che nella tabella Classi!)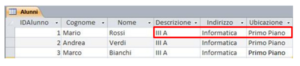
Problema 3: se Rossi cambia classe devo aggiornare tutti e tre i campi collegati alla classe.
I tre problemi elencati in precedenza possono essere risolti definendo una relazione tra le tabelle.
Nella tabella Alunni basta aggiungere il solo campo “Classe” che rappresenta il legame con la tabella Classi
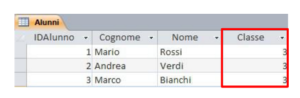
Il campo “Classe” della tabella Alunni è in relazione con il campo “IDClasse” della tabella Classi
I dati della classe saranno gestiti solo nella tabella Classi
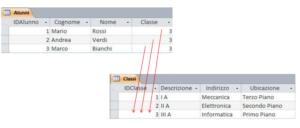
| Problema 1:
ho una gran quantità di dati ripetuti che aumentano notevolmente la dimensione del database |
Problema 1 – risolto:
nella tabella alunni memorizzo solo un codice numerico che fa riferimento alla tabella Classi |
| Problema 2:
se la classe III A subisce uno spostamento di piano devo riorganizzare i record correlati |
Problema 2 – risolto:
devo modificare solo il campo ubicazione nella tabella Classi |
| Problema 3:
se Rossi cambia classe devo aggiornare tutti e tre i campi collegati alla classe |
Problema 3 – risolto:
devo modificare per Rossi solo il campo codice nella tabella Classi |
TIPI DI RELAZIONI
Relazione UNO A MOLTI:
un record della prima tabella è associato a più record dell’altra
Uno-a-molti Si ha quando un elemento di una tabella può avere una relazione con più elementi di un’altra tabella. Ad esempio, ogni ordine d’acquisto può includere più prodotti.
Una delle relazioni più comuni tra le tabelle di un database ben progettato è la relazione uno-a-molti.
La relazione che usi dipende dai dati. Una relazione uno-a-molti avviene quando un singolo record in una tabella è correlato a uno o più record in un’altra tabella.
Relazione UNO A UNO:
ogni record della prima tabella può avere solo un record corrispondente nella seconda tabella e viceversa
Uno-a-uno Si ha quando ogni elemento in ciascuna tabella compare una sola volta. Ad esempio, ogni dipendente può avere una sola auto aziendale da usare.
Una relazione uno-a-uno è un collegamento tra le informazioni contenute in due tabelle, dove ogni record in ciascuna tabella compare una sola volta. Ad esempio, potrebbe esistere una relazione uno-a-uno tra i dipendenti e le auto che guidano. Ogni dipendente compare una sola volta nella tabella Dipendenti e ogni auto compare una sola volta nella tabella Auto aziendali.
Relazione MOLTI A MOLTI:
a ogni record della prima tabella possono corrispondere più record della seconda tabella e viceversa.
Molti-a-molti. Si ha quando uno o più elementi di una tabella possono avere una relazione con uno o più elementi di un’altra tabella. Ad esempio, ogni ordine può avere più prodotti e ogni prodotto può essere incluso in più ordini.
Le relazioni molti-a-molti sono le relazioni tra tabelle più usate. Forniscono informazioni cruciali, ad esempio quali clienti sono stati contattati dal personale di vendita e quali prodotti sono inclusi negli ordini dei clienti.
Una relazione molti-a-molti si ha quando uno o più elementi di una tabella possono avere una relazione con uno o più elementi di un’altra tabella.
COME SI CREANO LE RELAZIONI?
- Aprire un database ed arricchirlo con campi e relativi dati
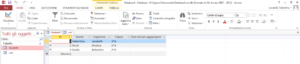
b. Nell’etichetta “Strumenti database” fare clic su “Relazioni”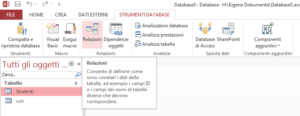
c. Selezionare nella finestra che compare, le due tabelle e fare clic su “Chiudi”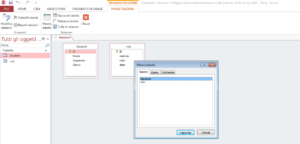
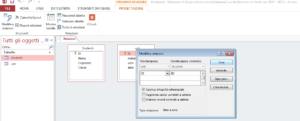
d. Trascinare il campo “IDvoti” nella tabella “Studenti”.
e. Nella finestra a comparsa, spuntare il quadrato “Applica integrità referenziale”, fare clic su “Crea”.
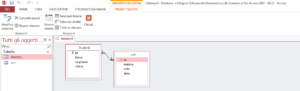
f. Automaticamente avremo la relazione creata da Access.
Questo post è creato da Valentina Locatelli e Nicol Modica
[:]
![]() [:]
[:]


















 al suo interno si selezione Relazioni.
al suo interno si selezione Relazioni.