SCIENZE E TECNOLOGIE INFORMATICHE

[:it]

Jorge Ignacio Nazabal

Per potere essere in grado di calcolare il minimo comune multiplo (m.c.m.) o il Massimo Comune Divisore (M.C.D.) tra due o più numeri, si deve essere in grado di effettuare la scomposizione dei numeri stessi.

Euclide ha postulato il seguente TEOREMA FONDAMENTALE DELL’ALGEBRA

Ogni numero composto può essere scritto, in modo unico, come prodotto di fattori primi

L’operazione che consente di scrivere un numero composto come prodotto di fattori primi si chiama scomposizione in fattori primi (o fattorizzazione).

I divisori, ossia i numeri che dividono il numero da scomporre, devono essere numeri primi.

I numeri primi che normalmente si usano sono i seguenti:

1 , 2,  3 , 5 , 7 , 11 , 13

in seguito alla scomposizione precedente il numero

l’esponente del è perché vi sono due 2, l’esponente del 3 è 4 perché vi sono quattro 3 nella colonna di destra.

Altri esempi:

quindi

.

Il m.c.m. (minimo comune multiplo) è il numero più piccolo che contiene (ossia è multiplo) dei numeri di cui si vuole calcolare il m.c.m.

Cosa fare per trovarlo?

• si scompongono i numeri
• si prendono i numeri comuni  con l’esponente più alto
• si prendono i numeri NON comuni con l’esponente più alto
• si moltiplicano tra di loro i numeri dei due punti precedenti

Esempio.

trovare il m.c.m. tra 4 e 6.

• scompongo i due numeri

• prendo i numeri comuni con l’esponente più alto ossia il
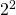
• prendo i numeri comuni con l’esponente più alto ossia il

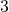
il mc.m. è:

Un metodo pratico può essere:

• prendere il numero più grande tra quelli di cui si vuole trovare il m.c.m.
• fare la tabellina di questo numero e verificare ogni volta se questo è divisibile per gli altri numeri. (divisibile significa che mi deve dare un numero senza resto).

applicandolo all’esempio precedente:

• prendo il 6
• faccio
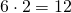
• 12 è divisibile per 4 per cui è proprio il m.c.m.

Il M.C.D. (Massimo Comune Divisore) è il numero più grande che divide esattamente tutti i numeri dati.

Cosa fare per trovarlo?

• si scompongono i numeri in fattori primi
• si prendono solo i numeri comuni con l’esponente più basso
• si moltiplicano tra di loro i numeri del punto precedente

Sviluppando l’esercizio precedente si ha:

• prendo il numero comune

ossia il 2 ed è proprio il M.C.D.[:]

[:it]

Ricardo Fernandez Ortega

Questa verifica è il primo passo per verificare le proprie competenze di base sulle equazioni di primo grado.

Buon lavoro.

[WpProQuiz 23][:]

Jacek Yerka

Una delle potenzialità di access, oltre quella di creare tabelle è quella di eseguire delle interrogazioni o meglio delle query sul database.

Per fare delle interrogazione bisogna imparare a scrivere nel linguaggio “access” le richieste.

Ad esempio se si ha la necessità di avere l’elenco delle persone che abitano in un’opportuna città è necessario scrivere nei criteri = ‘Bolzano’.

L’elenco completo con opportuni esempi è presente al seguente link

Criteri di ricerca

[:it]

Jacek Yerka

Tale verifica è strutturata in maniera tale da dare un peso diverso alle domande nel senso che vi sono al suo interno domande poste in maniera graduale ma di complessità diversa. Il gran numero di domande permette di arrivare alla sufficienza, per l’ottimo vi sono domande più complesse.
[WpProQuiz 22][:]

7 esercizi:

7-esercizi-word

[:it]

Renè Magritte

La prima regola, che permette di risolvere le equazioni di primo grado, può essere riassunta con quest’affermazione che deriva dalle riflessioni dei paragrafi precedenti.

Siccome è una pietra miliare, mi preme sempre ricordarla: l’operazione che viene effettuata a destra deve essere uguale a quella a sinistra.

Ciò non toglie che l’affermazione seguente sia valida:

quando un numero o l’incognita “attraversa” l’uguale esso o essa cambia di segno ossia se era positiva esso o essa diventa negativa e viceversa.

Ad esempio:

3+x=5

è equivalente alle seguenti equazioni

Questa regola “empirica”, ossia dettata dallo sviluppo pratico, la si utilizza per risolvere questo tipo di equazioni di primo grado:

3+x=-x+5

infatti devo raggruppare le x a sinistra e i numeri a destra

x+x=5-3

sommo le x ed ho:

che applicando la seconda regola, ossia dividendo a sinistra ed a destra per 2, risulta:

x=1.[:]

1. Apri il programma Access
2. Nomina il database Cinema
   

   Jacek Yerka

3. Crea la tabella cinema
4. Crea i seguenti campi nella tabella cinema in visualizza struttura:
   1. la chiave primaria è un contatore,

le altre colonne saranno numero biglietto, tipo di biglietto, costo, titolo film, trailer

1. Numero biglietto
   1.   numerico intero,
   2. descrizione: numero del biglietto,
   3. formato, numero generico,
   4. valido solo per valori postivi (>0),
   5. messaggio d’errore “Solo valori positivi”,
   6. non valori duplicati
2. Tipo Biglietto
   1. testo ,
   2. dimensione campo 20,
   3. valore predefinito: “intero”,
   4. sempre richiesto,
   5. consenti lunghezza zero no.
3. costo:
   1. tipo valuta,
   2. decimali 2,
   3. valido solo se sono inseriti valori più grandi di zero
4. titolo film:
   1. di tipo testo ,
   2. dimensione 200,
5. trailer
   1. : di tipo testo lungo
6. Crea una maschera per l’inserimento dei dati escludendo il campo chiave
7.  Inserisci almeno tre record, nel campo trailer. Inserisci l’indirizzo URL di un trailer esistente.
8. Verifica la correttezza del tipo di dati e dei valori predefiniti

[:it]1.

2.

3.

4.

5.

6.

7.

8.

9.

 [:]

[:it]Esercizi sulla prima regola.

Trovare il valore di x.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Esercizi sulla seconda regola.

Trovare il valore di x

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

Esercizi sulla terza regola

Trovare il valore di x

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8. 

3.9.

3.10. [:]

[:it]I regola – Macchina a 7 posti

Un’automobile ha 7 posti, di cui 3 sono già occupati. Quante altre persone vi possono salire?

Questo problema si può risolvere in questa maniera:

Posti già occupati + Posti liberi = Posti Totali

3 + Posti Liberi = 7

Siccome un’equazione di primo grado deve essere pensata come una bilancia il cui fulcro rappresenta il segno di uguale. Nei due bracci della bilancia vi sono i pesi che devono stare in equilibrio.

Per risolvere il problema precedente faccio la seguente operazione:

• sottraggo da entrambi i membri il numero 3 in maniera tale che a sinistra compaiano solo i Posti Liberi:

-3 +3 + Posti Liberi = 7 -3

-3 e +3 sono opposti e la loro somma mi dà il numero 0.

Posti Liberi = 7-3=4

In termini matematici posso pensare alla seguente equazione:

3+x=7

x=7-3=4

dove x rappresenta i Posti Liberi

II Regola – Costo di una mela

7 mele costano 14€. Quanto costa una mela?

Schematizzando il problema precedente ho:

7 mele= 14

Per risolvere il problema divido per 7 sia a destra che a sinistra:

e quindi una mela costa 2€ perché 14 diviso 7 fa 2.

In termini matematici ho la seguente equazione:

dove la x rappresenta le mele.

III Regola – il conto

Vi sono 3 persone che pagano 20€ ciascuna il conto della pizza. Si vuole sapere quant’era il conto.

Il problema si risolve mediante questa equazione:

Per risolvere il problema moltiplico a sinistra e a destra per 3 ossia:

e quindi il conto è di 60€.

In termini matematici si esprime:

dove con la x indico il conto.[:]