[:it]

Rafal Olbinski
In assenza di variabilità, in una popolazione, la statistica non sarebbe necessaria: un singolo elemento o unità campionaria sarebbe sufficiente a determinare tutto ciò che occorre sapere su una popolazione.
Ne consegue, perciò, che nel presentare informazioni su un campione non è sufficiente fornire semplicemente una misura della media ma servono informazioni sulla variabilità.
Si considera la seguente tabella che mostra l’età di due gruppi
| Soggetto |
I gruppo |
II gruppo |
| 1 |
20 |
10 |
| 2 |
30 |
25 |
| 3 |
40 |
40 |
| 4 |
50 |
55 |
| 5 |
60 |
70 |
| media |
40 |
40 |
Si può subito notare che la media mi fornisce lo stesso valore, ma se suppongo di avere un ristorante e devo preparare dei menù, sapendo che hanno la stessa età media i due gruppi allora lo preparo uguale.
Sarebbe un grave errore se non prendessi in considerazione la variabilità. Infatti se nel primo gruppo potrebbe andare bene un menù per adulti nel secondo vi è un bambino a cui magari si dovrebbe adattarlo.
Allora si introducono tre misure di variabilità:
- campo di variazione
- varianza
- deviazione standard
Il campo di variazione corrisponde alla differenza fra il valore più piccolo e quello più grande:
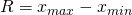
Il limite di tale valore è:
- è influenzato dai valori estremi
- tiene conto dei due soli valori estremi, trascurando tutti gli altri.
La varianza è data dalla somma dei quadrati degli scarti dalla media diviso per il numero degli elementi.
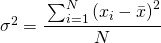
mentre la deviazione standard è la radice quadrata della varianza ossia:
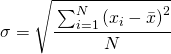
La varianza mi fornisce un indice di dispersione dei dati rispetto alla media ed ha il vantaggio che, essendo un quadrato, non è influenzata da dati negativi che sommandosi si annullerebbero.
Lo svantaggio è che essendo un quadrato non presenta la stessa unità di misura dei dati per cui si preferisce sempre la sua radice quadrata che è appunto la deviazione standard.
[:en]

Rafel Olbinski
In assenza di variabilità, in una popolazione, la statistica non sarebbe necessaria: un singolo elemento o unità campionaria sarebbe sufficiente a determinare tutto ciò che occorre sapere su una popolazione.
Ne consegue, perciò, che nel presentare informazioni su un campione non è sufficiente fornire semplicemente una misura della media ma servono informazioni sulla variabilità.
Si considera la seguente tabella che mostra l’età di due gruppi
| Soggetto |
I gruppo |
II gruppo |
| 1 |
20 |
10 |
| 2 |
30 |
25 |
| 3 |
40 |
40 |
| 4 |
50 |
55 |
| 5 |
60 |
70 |
| media |
40 |
40 |
Si può subito notare che la media mi fornisce lo stesso valore, ma se suppongo di avere un ristorante e devo preparare dei menù, sapendo che hanno la stessa età media i due gruppi allora lo preparo uguale.
Sarebbe un grave errore se non prendessi in considerazione la variabilità. Infatti se nel primo gruppo potrebbe andare bene un menù per adulti nel secondo vi è un bambino a cui magari si dovrebbe adattarlo.
Allora si introducono tre misure di variabilità:
- campo di variazione
- varianza
- deviazione standard
Il campo di variazione corrisponde alla differenza fra il valore più piccolo e quello più grande:
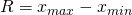
Il limite di tale valore è:
- è influenzato dai valori estremi
- tiene conto dei due soli valori estremi, trascurando tutti gli altri.
La varianza è data dalla somma dei quadrati degli scarti dalla media diviso per il numero degli elementi.
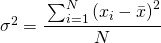
mentre la deviazione standard è la radice quadrata della varianza ossia:
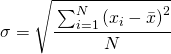
La varianza mi fornisce un indice di dispersione dei dati rispetto alla media ed ha il vantaggio che, essendo un quadrato, non è influenzata da dati negativi che sommandosi si annullerebbero.
Lo svantaggio è che essendo un quadrato non presenta la stessa unità di misura dei dati per cui si preferisce sempre la sua radice quadrata che è appunto la deviazione standard.
[:de]

Rafel Olbinski
In assenza di variabilità, in una popolazione, la statistica non sarebbe necessaria: un singolo elemento o unità campionaria sarebbe sufficiente a determinare tutto ciò che occorre sapere su una popolazione.
Ne consegue, perciò, che nel presentare informazioni su un campione non è sufficiente fornire semplicemente una misura della media ma servono informazioni sulla variabilità.
Si considera la seguente tabella che mostra l’età di due gruppi
| Soggetto |
I gruppo |
II gruppo |
| 1 |
20 |
10 |
| 2 |
30 |
25 |
| 3 |
40 |
40 |
| 4 |
50 |
55 |
| 5 |
60 |
70 |
| media |
40 |
40 |
Si può subito notare che la media mi fornisce lo stesso valore, ma se suppongo di avere un ristorante e devo preparare dei menù, sapendo che hanno la stessa età media i due gruppi allora lo preparo uguale.
Sarebbe un grave errore se non prendessi in considerazione la variabilità. Infatti se nel primo gruppo potrebbe andare bene un menù per adulti nel secondo vi è un bambino a cui magari si dovrebbe adattarlo.
Allora si introducono tre misure di variabilità:
- campo di variazione
- varianza
- deviazione standard
Il campo di variazione corrisponde alla differenza fra il valore più piccolo e quello più grande:
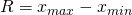
Il limite di tale valore è:
- è influenzato dai valori estremi
- tiene conto dei due soli valori estremi, trascurando tutti gli altri.
La varianza è data dalla somma dei quadrati degli scarti dalla media diviso per il numero degli elementi.
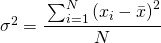
mentre la deviazione standard è la radice quadrata della varianza ossia:
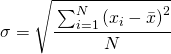
La varianza mi fornisce un indice di dispersione dei dati rispetto alla media ed ha il vantaggio che, essendo un quadrato, non è influenzata da dati negativi che sommandosi si annullerebbero.
Lo svantaggio è che essendo un quadrato non presenta la stessa unità di misura dei dati per cui si preferisce sempre la sua radice quadrata che è appunto la deviazione standard.
[:]
![]() scrivere i seguenti prodotti utilizzando le potenze:
scrivere i seguenti prodotti utilizzando le potenze:

 Allego il file in cui ho sviluppato tutti gli esercizi, la teoria necessaria i prerequisiti della prova di matematica dell’anno 2016.
Allego il file in cui ho sviluppato tutti gli esercizi, la teoria necessaria i prerequisiti della prova di matematica dell’anno 2016. Ecco il file con il testo:
Ecco il file con il testo: [:]
[:]
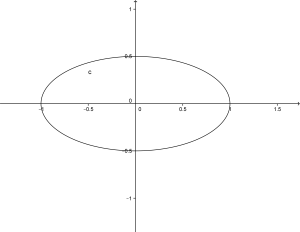
 6.1
6.1
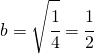
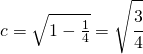
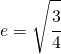

![Rendered by QuickLaTeX.com \left [ \cfrac{4}{\sqrt{3}};12 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5c87560651d92e6ddc58fae10715b0d4_l3.png)
![Rendered by QuickLaTeX.com \left [\cfrac{x^2}{100}+\cfrac{y^2}{64}=1 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-db4a27f5148afa23d64f35bf50b1869e_l3.png)
![Rendered by QuickLaTeX.com \left [\cfrac{x^2}{36}+\cfrac{y^2}{100}=1 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4394ec2c524d27801983334d705a5b57_l3.png)