[:it]

Rafal Olbinski
La mediana (Me) è quel dato che divide l’insieme dei dati in due parti uguali.
L’idea che è alla base della mediana è quella di cercare un numero che sia più grande di un 50% delle osservazioni e più piccolo del restante 50%.
Spero con un esempio di chiarire il concetto:
Dati i seguenti valori:
71, 81, 90, 92, 94, 96, 97
Per trovare la mediana devo contare i valori che sono 7:
Il valore che sta esattamente nel mezzo è il 92 infatti esso ha alla sua sinistra 3 valori ed alla sua destra altri 3.
Quindi si deve pensare più che al valore di per sé alla sua posizione.
Per determinare quale valore prendere si prende quel valore che si trova alla posizione:
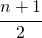
con n il numero dei valori.
Relazione che vale se il numero di valori è dispari
nel caso dell’esempio il calcolo precedente risulta:
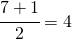
ossia devo prendere il valore che si trova alla posizione 4 che è appunto il 92.
Inserisco questa tabella per chiarire maggiormente il concetto:
| valore |
71 |
81 |
90 |
92 |
94 |
96 |
97 |
| posizione |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Nel caso in cui invece il numero di valori è pari quale valore prendere?
Si prendono i due valori che stanno nella posizione 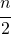 e
e 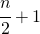 e si fa la loro media.
e si fa la loro media.
Un esempio spero che chiarisca il concetto.
Dati i valori
| Valore |
7 |
10 |
12 |
15 |
| Posizione |
1 |
2 |
3 |
4 |
n=4 che è pari per cui ho:
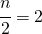 che corrisponde al valore 10.
che corrisponde al valore 10.
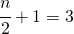 che corrisponde al valore 12.
che corrisponde al valore 12.
Adesso trovo la media tra questi due valori che è:
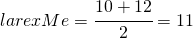
La moda è il valore che si presenta con maggiore frequenza.
Ad esempio dati i seguenti valori:
5,6,7,7,8.
La moda risulta 7 in quanto è il valore che si presenta con maggior frequenza.[:en]

Rafel Olbinski
La mediana (Me) è quel dato che divide l’insieme dei dati in due parti uguali.
L’idea che è alla base della mediana è quella di cercare un numero che sia più grande di un 50% delle osservazioni e più piccolo del restante 50%.
Spero con un esempio di chiarire il concetto:
Dati i seguenti valori:
71, 81, 90, 92, 94, 96, 97
Per trovare la mediana devo contare i valori che sono 7:
Il valore che sta esattamente nel mezzo è il 92 infatti esso ha alla sua sinistra 3 valori ed alla sua destra altri 3.
Quindi si deve pensare più che al valore di per sé alla sua posizione.
Per determinare quale valore prendere si prende quel valore che si trova alla posizione:
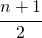
con n il numero dei valori.
Relazione che vale se il numero di valori è dispari
nel caso dell’esempio il calcolo precedente risulta:
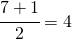
ossia devo prendere il calore che si trova alla posizione 4 che è appunto il 92.
Inserisco questa tabella per chiarire maggiormente il concetto:
| valore |
71 |
81 |
90 |
92 |
94 |
96 |
97 |
| posizione |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Nel caso in cui invece il numero di valori è pari quale valore prendere?
Si prendono i due valori che stanno nella posizione 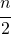 e
e 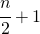 e si fa la loro media.
e si fa la loro media.
Un esempio spero che chiarisca il concetto.
Dati i valori
| Valore |
7 |
10 |
12 |
15 |
| Posizione |
1 |
2 |
3 |
4 |
n=4 che è pari per cui ho:
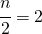 che corrisponde al valore 10.
che corrisponde al valore 10.
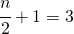 che corrisponde al valore 12.
che corrisponde al valore 12.
Adesso trovo la media tra questi due valori che è:
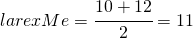
La moda è il valore che si presenta con maggiore frequenza.
Ad esempio dati i seguenti valori:
5,6,7,7,8.
La moda risulta 7 in quanto è il valore che si presenta con maggior frequenza.[:de]

Rafel Olbinski
La mediana (Me) è quel dato che divide l’insieme dei dati in due parti uguali.
L’idea che è alla base della mediana è quella di cercare un numero che sia più grande di un 50% delle osservazioni e più piccolo del restante 50%.
Spero con un esempio di chiarire il concetto:
Dati i seguenti valori:
71, 81, 90, 92, 94, 96, 97
Per trovare la mediana devo contare i valori che sono 7:
Il valore che sta esattamente nel mezzo è il 92 infatti esso ha alla sua sinistra 3 valori ed alla sua destra altri 3.
Quindi si deve pensare più che al valore di per sé alla sua posizione.
Per determinare quale valore prendere si prende quel valore che si trova alla posizione:
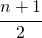
con n il numero dei valori.
Relazione che vale se il numero di valori è dispari
nel caso dell’esempio il calcolo precedente risulta:
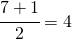
ossia devo prendere il calore che si trova alla posizione 4 che è appunto il 92.
Inserisco questa tabella per chiarire maggiormente il concetto:
| valore |
71 |
81 |
90 |
92 |
94 |
96 |
97 |
| posizione |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Nel caso in cui invece il numero di valori è pari quale valore prendere?
Si prendono i due valori che stanno nella posizione 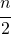 e
e 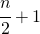 e si fa la loro media.
e si fa la loro media.
Un esempio spero che chiarisca il concetto.
Dati i valori
| Valore |
7 |
10 |
12 |
15 |
| Posizione |
1 |
2 |
3 |
4 |
n=4 che è pari per cui ho:
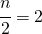 che corrisponde al valore 10.
che corrisponde al valore 10.
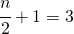 che corrisponde al valore 12.
che corrisponde al valore 12.
Adesso trovo la media tra questi due valori che è:
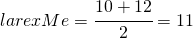
La moda è il valore che si presenta con maggiore frequenza.
Ad esempio dati i seguenti valori:
5,6,7,7,8.
La moda risulta 7 in quanto è il valore che si presenta con maggior frequenza.[:]






![Rendered by QuickLaTeX.com \left [ \cfrac{3\sqrt{15}}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c1fef64c2c870c09c550a985b9df9f75_l3.png)


![Rendered by QuickLaTeX.com \left [\sqrt{\cfrac{1}{12}}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7bf62ee257f721d5197f0c02371b95af_l3.png)
![Rendered by QuickLaTeX.com -\cfrac{2}{5}\sqrt[3]{\cfrac{25}{4}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f8eb0a1626f86182bdebb0d0de4211ce_l3.png)
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{5}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-116d97c34f9ce9c78d11eb68baf7d238_l3.png)
![Rendered by QuickLaTeX.com -\frac{1}{2}\sqrt[3]{\cfrac{40}{3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-16e61c2921dbdbe8e5cf5ab140d9fcbb_l3.png)
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{5}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-0300581f825606a4df561791b959784d_l3.png)
![Rendered by QuickLaTeX.com -\cfrac{4}{3}\sqrt[3]{\cfrac{9}{32}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-98662ced01fc9c0f6667680cec8b50f0_l3.png)
![Rendered by QuickLaTeX.com \left [-\sqrt[3]{\cfrac{2}{3}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a2e8a6fda45f51f4d757ab599f211f1a_l3.png)
![Rendered by QuickLaTeX.com -\cfrac{3}{4}\sqrt[3]{\cfrac{4}{9}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-32123463fa31c8f9543ab093139135c6_l3.png)
![Rendered by QuickLaTeX.com \left [ -\sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3081a84110f7fbcd3efe5cd77db53175_l3.png)
![Rendered by QuickLaTeX.com \cfrac{2}{3}\sqrt[2]{2-\cfrac{7}{8}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3a2cce9a34148ff74aabc3a10a539306_l3.png)
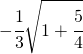
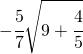

![Rendered by QuickLaTeX.com \cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72a4779832adecc9db54627aff579e61_l3.png)
![Rendered by QuickLaTeX.com \left [ \sqrt[3]{\cfrac{3}{16}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-26c97c3c1e73806b4efe438114e712dc_l3.png)
![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9a^2b^4}{16c^6}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f10b03216b38445efffe2dd12bd5369f_l3.png)
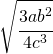
![Rendered by QuickLaTeX.com \sqrt[4]{\cfrac{9}{16}+\cfrac{3}{2}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-faee1149f7b9e8ae04313342cb2e71f2_l3.png)
![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{25}{9}-\cfrac{10}{3}+1}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-728aac4ec645636813f7a66481d305f6_l3.png)
![Rendered by QuickLaTeX.com \sqrt[2]{\cfrac{9}{49}+\cfrac{12}{7}+4}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-057c824034125a2021e9350be7484684_l3.png)
![Rendered by QuickLaTeX.com \sqrt[6]{\cfrac{x^2-10x+25}{x^2-8xy+16y^2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f64a34efd752c1499f92daa202280468_l3.png)
![Rendered by QuickLaTeX.com \left [\sqrt[3]{\cfrac{x-5}{x-4y}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-c36847a763bf12a84b44dd7b03aa530e_l3.png)
![Rendered by QuickLaTeX.com \sqrt[9]{\cfrac{27a^3b^6}{\left ( 81a^2-18a+1 \right )^3}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25f05ba22d0f46215979fa4ec827a23e_l3.png)
![Rendered by QuickLaTeX.com \left [ \cfrac{3ab^2}{\left ( 9a-1 \right )^2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-22dadf3866a664b2c64062d013cdfc69_l3.png)



![Rendered by QuickLaTeX.com \left[\cfrac{7}{x+2}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-54046183c8ce402bd873f3fe1da73dcd_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{6x}{x+2y}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25e15a79e3953112dfde74a771ae9a83_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{2a}{a+1}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-87dc784053b1a3af04255d5559c124c5_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{1-x}{a-x^2}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3191b1f9c9d953f51225a43cc7645b1_l3.png)