[:it]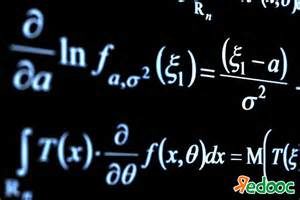 Allego il file in cui ho sviluppato tutti gli esercizi, la teoria necessaria i prerequisiti della prova di matematica dell’anno 2016.
Allego il file in cui ho sviluppato tutti gli esercizi, la teoria necessaria i prerequisiti della prova di matematica dell’anno 2016.
Per chi avesse ancora qualche dubbio mi contatti.Provadimatematica2016
[:]

[:it]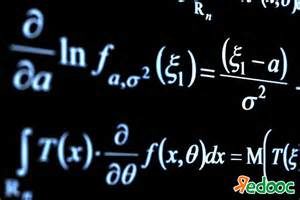 Allego il file in cui ho sviluppato tutti gli esercizi, la teoria necessaria i prerequisiti della prova di matematica dell’anno 2016.
Allego il file in cui ho sviluppato tutti gli esercizi, la teoria necessaria i prerequisiti della prova di matematica dell’anno 2016.
Per chi avesse ancora qualche dubbio mi contatti.Provadimatematica2016
[:]
[:it]Oggi 12 maggio 2016 si tengono le prove INVALSI di matematica, il lavoro di un intero biennio di matematica viene messo alla prova sia per gli studenti che per gli insegnanti.
 [:]
[:]
[:it]

Yves Tanguy
I voti presi da uno studente nel primo quadrimestre sono 6, 7, 5, 6, 6, 7, 4, 5, 6, 7, 7, 7, 4, 7. Calcola la sua media dei voti, la mediana e la moda. [6;6;7]
La seguente tabella raccoglie i valori dei salari giornalieri di un gruppo di 20 operai di una fabbrica.
| salario | 20 | 25 | 30 |
| frequenza | 10 | 6 | 4 |
Calcola la media, la mediana e la moda di tali salari. [23,50€; 22.50€; 20€]
3. Data la sequenza di numeri 8, 3, 14, 6, 9, 3, 3, 5, 2, 3, 8, 8, determina la media, la mediana e la moda. [6; 5,5; 3]
4. Si è rilevato che un determinato tipo di frigorifero ha prezzi che variano a seconda del punto di vendita. I valori rilevati sono esposti nella seguente tabella.
| Prezzo | 380 | 399 | 420 | 435 | 444 |
| N.venditori | 3 | 4 | 2 | 1 | 1 |
Calcola la media, la mediana la moda.
5.Data la seguente tabella dei redditi da pensione di un campione di 100 persone, calcola la media aritmetica e individua la classe nella quale è compresa la mediana.
| Importo | 500-700 | 700-900 | 900-1200 | 1200-1500 | 1500-2000 | 2000-2500 |
| N. Pensionati | 26 | 32 | 22 | 12 | 6 | 2 |
[955; classe 700-900]
[:]
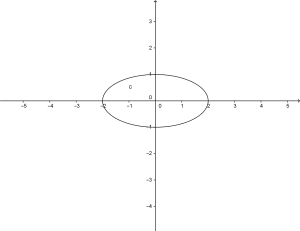
[:it] 6.1
6.1
L’equazione generica dell’ellisse è:
![]()
e confrontandola con quella dell’esercizio
![]()
si nota immediatamente che
![]()
![]()
ed ho quindi trovato i vertici dell’ellisse che sono i punti in cui l’ellisse interseca l’asse delle ascisse e l’asse delle ordinate.
+a e -a sono le intersezioni con l’asse delle ascisse
+b e -b sono le intersezioni con l’asse delle ordinate
per trovare qual è l’asse maggiore si confrontano i punti a e b e si nota che a che vale 2 è maggiore di b che vale 1.
Per trovare le coordinate dei fuochi si usa la seguente formula:
![]()
sostituendo alle lettere i rispettivi valori si ha:
![]()
determinata la c posso trovare l’eccentricità che mi fornisce di quanto la mia ellisse sia “schiacciata”
![]()
Adesso posso disegnare l’ellisse il cui grafico risulta:
7.1.
Confronto
![]()
con la forma canonica
![]()
noto subito che nell’esercizio devo manipolare il coefficiente che moltiplica ![]() in questa maniera:
in questa maniera:
![]()
così posso subito identificare:
![]()
e
![]()
quindi ![]() e
e 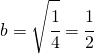
Le coordinate dei fuochi
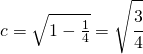
ed infine l’eccentricità
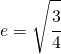
il grafico di questa ellisse risulta:
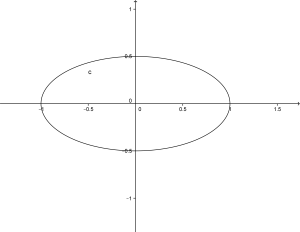
8.1.
Confronto
![]()
con l’equazione canonica
![]()
mi devo trovar l’uno, per cui diviso a sinistra e a destra per 25 e quindi l’equazione di partenza risulta.
[:]
[:it]

Jim Warren
Ricapitolando.
Un’ellisse è caratterizzata dai sui vertici, dalle coordinate dei fuochi, dall’eccentricità.
Per poterla disegnare si annulla prima la x e si trovano le intersezioni con l’asse y e viceversa.
Rappresentare graficamente le seguenti ellissi, dopo aver determinato, di ciascuna di esse, le coordinate dei vertici, quelle dei fuochi e l’eccentricità.
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
|
| 6.5. Determina la misura degli assi dell’ellisse:
|
|
| 6.6.Determina le coordinate dei fuochi dell’ellisse: |
Esercizi per un livello discreto (7):
| 7.1. |
|
| 7.2. |
|
| 7.3. |
|
| 7.4. Determina la misura degli assi dell’ellisse:
|
![Rendered by QuickLaTeX.com \left [ \cfrac{4}{\sqrt{3}};12 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5c87560651d92e6ddc58fae10715b0d4_l3.png) |
| 7.5. Determina le cocordinate dei fuochi: |
Esercizi per un buon livello (8)
| 8.1. |
| 8.2. |
| 8.3. |
| 9.1. Determina l’equazione del luogo geometrico dei punti tali che la somma delle distanze dai punti |
![Rendered by QuickLaTeX.com \left [\cfrac{x^2}{100}+\cfrac{y^2}{64}=1 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-db4a27f5148afa23d64f35bf50b1869e_l3.png) |
| 9.2. Determina l’equazione del luogo geometrico dei punti tali che la somma delle distanze dai punti |
![Rendered by QuickLaTeX.com \left [\cfrac{x^2}{36}+\cfrac{y^2}{100}=1 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4394ec2c524d27801983334d705a5b57_l3.png) |
soluzioni[:en]

Jim Warren
Ricapitolando.
Un’ellisse è caratterizzata dai sui vertici, dalle coordinate dei fuochi, dall’eccentricità.
Per poterla disegnare si annulla prima la x e si trovano le intersezioni con l’asse y e viceversa.
Rappresentare graficamente le seguenti ellissi, dopo aver determinato, di ciascuna di esse, le coordinate dei vertici, quelle dei fuochi e l’eccentricità.
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
Esercizi per un livello discreto (7):
| 7.1. |
| 7.2. |
| 7.3. |
Esercizi per un buon livello (8)
| 8.1. |
| 8.2. |
| 8.3. |
[:de]

Jim Warren
Ricapitolando.
Un’ellisse è caratterizzata dai sui vertici, dalle coordinate dei fuochi, dall’eccentricità.
Per poterla disegnare si annulla prima la x e si trovano le intersezioni con l’asse y e viceversa.
Rappresentare graficamente le seguenti ellissi, dopo aver determinato, di ciascuna di esse, le coordinate dei vertici, quelle dei fuochi e l’eccentricità.
Esercizi per un livello sufficiente (6):
| 6.1. |
|
| 6.2. |
|
| 6.3. |
|
| 6.4. |
Esercizi per un livello discreto (7):
| 7.1. |
| 7.2. |
| 7.3. |
Esercizi per un buon livello (8)
| 8.1. |
| 8.2. |
| 8.3. |
[:]
[:it]

Rafal Olbinski
In assenza di variabilità, in una popolazione, la statistica non sarebbe necessaria: un singolo elemento o unità campionaria sarebbe sufficiente a determinare tutto ciò che occorre sapere su una popolazione.
Ne consegue, perciò, che nel presentare informazioni su un campione non è sufficiente fornire semplicemente una misura della media ma servono informazioni sulla variabilità.
Si considera la seguente tabella che mostra l’età di due gruppi
| Soggetto | I gruppo | II gruppo |
| 1 | 20 | 10 |
| 2 | 30 | 25 |
| 3 | 40 | 40 |
| 4 | 50 | 55 |
| 5 | 60 | 70 |
| media | 40 | 40 |
Si può subito notare che la media mi fornisce lo stesso valore, ma se suppongo di avere un ristorante e devo preparare dei menù, sapendo che hanno la stessa età media i due gruppi allora lo preparo uguale.
Sarebbe un grave errore se non prendessi in considerazione la variabilità. Infatti se nel primo gruppo potrebbe andare bene un menù per adulti nel secondo vi è un bambino a cui magari si dovrebbe adattarlo.
Allora si introducono tre misure di variabilità:
Il campo di variazione corrisponde alla differenza fra il valore più piccolo e quello più grande:
![]()
Il limite di tale valore è:
La varianza è data dalla somma dei quadrati degli scarti dalla media diviso per il numero degli elementi.
![]()
mentre la deviazione standard è la radice quadrata della varianza ossia:
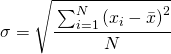
La varianza mi fornisce un indice di dispersione dei dati rispetto alla media ed ha il vantaggio che, essendo un quadrato, non è influenzata da dati negativi che sommandosi si annullerebbero.
Lo svantaggio è che essendo un quadrato non presenta la stessa unità di misura dei dati per cui si preferisce sempre la sua radice quadrata che è appunto la deviazione standard.
[:en]

Rafel Olbinski
In assenza di variabilità, in una popolazione, la statistica non sarebbe necessaria: un singolo elemento o unità campionaria sarebbe sufficiente a determinare tutto ciò che occorre sapere su una popolazione.
Ne consegue, perciò, che nel presentare informazioni su un campione non è sufficiente fornire semplicemente una misura della media ma servono informazioni sulla variabilità.
Si considera la seguente tabella che mostra l’età di due gruppi
| Soggetto | I gruppo | II gruppo |
| 1 | 20 | 10 |
| 2 | 30 | 25 |
| 3 | 40 | 40 |
| 4 | 50 | 55 |
| 5 | 60 | 70 |
| media | 40 | 40 |
Si può subito notare che la media mi fornisce lo stesso valore, ma se suppongo di avere un ristorante e devo preparare dei menù, sapendo che hanno la stessa età media i due gruppi allora lo preparo uguale.
Sarebbe un grave errore se non prendessi in considerazione la variabilità. Infatti se nel primo gruppo potrebbe andare bene un menù per adulti nel secondo vi è un bambino a cui magari si dovrebbe adattarlo.
Allora si introducono tre misure di variabilità:
Il campo di variazione corrisponde alla differenza fra il valore più piccolo e quello più grande:
![]()
Il limite di tale valore è:
La varianza è data dalla somma dei quadrati degli scarti dalla media diviso per il numero degli elementi.
![]()
mentre la deviazione standard è la radice quadrata della varianza ossia:
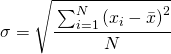
La varianza mi fornisce un indice di dispersione dei dati rispetto alla media ed ha il vantaggio che, essendo un quadrato, non è influenzata da dati negativi che sommandosi si annullerebbero.
Lo svantaggio è che essendo un quadrato non presenta la stessa unità di misura dei dati per cui si preferisce sempre la sua radice quadrata che è appunto la deviazione standard.
[:de]

Rafel Olbinski
In assenza di variabilità, in una popolazione, la statistica non sarebbe necessaria: un singolo elemento o unità campionaria sarebbe sufficiente a determinare tutto ciò che occorre sapere su una popolazione.
Ne consegue, perciò, che nel presentare informazioni su un campione non è sufficiente fornire semplicemente una misura della media ma servono informazioni sulla variabilità.
Si considera la seguente tabella che mostra l’età di due gruppi
| Soggetto | I gruppo | II gruppo |
| 1 | 20 | 10 |
| 2 | 30 | 25 |
| 3 | 40 | 40 |
| 4 | 50 | 55 |
| 5 | 60 | 70 |
| media | 40 | 40 |
Si può subito notare che la media mi fornisce lo stesso valore, ma se suppongo di avere un ristorante e devo preparare dei menù, sapendo che hanno la stessa età media i due gruppi allora lo preparo uguale.
Sarebbe un grave errore se non prendessi in considerazione la variabilità. Infatti se nel primo gruppo potrebbe andare bene un menù per adulti nel secondo vi è un bambino a cui magari si dovrebbe adattarlo.
Allora si introducono tre misure di variabilità:
Il campo di variazione corrisponde alla differenza fra il valore più piccolo e quello più grande:
![]()
Il limite di tale valore è:
La varianza è data dalla somma dei quadrati degli scarti dalla media diviso per il numero degli elementi.
![]()
mentre la deviazione standard è la radice quadrata della varianza ossia:
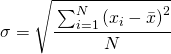
La varianza mi fornisce un indice di dispersione dei dati rispetto alla media ed ha il vantaggio che, essendo un quadrato, non è influenzata da dati negativi che sommandosi si annullerebbero.
Lo svantaggio è che essendo un quadrato non presenta la stessa unità di misura dei dati per cui si preferisce sempre la sua radice quadrata che è appunto la deviazione standard.
[:]

Thomas Barbey
Tutti questi problemi richiedono come conoscenza il concetto di probabilità come rapporto tra eventi favorevoli ed eventi probabili.
Per poterli risolvere bisogna prima sapere quanti sono gli eventi che si possono verificare, ad esempio il numero di palline all’interno di un cesto, il numero di studenti di una classe e poi contare quanti sono gli eventi che vogliamo sapere che possano accadere.
Ad esempio sapere qual è la probabilità che da un cesto di 100 palline possa estrarne 1 bianca sapendo che ve ne sono 40 di questo colore e le rimanenti di un altro, è un semplice rapporto ossia P(pallina bianca)=![]()
Esercizi per un livello base (6)
| 6.1. Lanciando due monete qual è la probabilità di ottenere due teste? | |
| 6.2. Vinco 1€ se nel lancio di un dado esce un numero superiore a 4. Quale probabilità ho di vincere? | |
| 6.3. Si lanciano due dadi. Trova la probabilità che escano due 3; che escano un 3 e un 4; che escano due numeri pari. | ![Rendered by QuickLaTeX.com \left [ \cfrac{1}{36};\cfrac{1}{18}; \cfrac{1}{4};\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3213078c1be67bffcb8d88653e5963a0_l3.png) |
| 6.4. Un’urna contiene 100 palline numerate da 1 a 100. Calcola la probabilità che una pallina estratta rechi un numero pari; un numero divisibile per 5; un numero divisibile per 6. | ![Rendered by QuickLaTeX.com \left [ \cfrac{1}{2};\cfrac{1}{5}; \cfrac{1}{25};\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-68e2ad8f9a3c88a0cf918ddbe900f67e_l3.png) |
| 6.5. Calcola qual è la probabilità di estrarre da un’urna contenente 5 palline bianche, 8 nere, 10 rosse, 12 verdi, una pallina bianca; una pallina nera; una pallina rossa; una pallina verde; una pallina o bianca o nera; una pallina o bianca o verde. | ![Rendered by QuickLaTeX.com \left [ \cfrac{1}{7};\cfrac{8}{35};\cfrac{2}{7};\cfrac{12}{35};\cfrac{13}{35};\cfrac{17}{35} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8ad7ac9876baa75fd6a8e3b6224f345e_l3.png) |
| 6.6. Calcola la probabilità che lanciando una moneta esca testa. | |
| 6.7. Calcola la probabilità che lanciando 1 dado esca il numero 1. | |
| 6.8. Calcola la probabilità che lanciando 1 dado esca un numero divisibile per 2. | |
| 6.9. Calcola la probabilità che lanciando 1 dado esca un numero multiplo di 3. |
Esercizi più complessi (7):
| Da un’urna contenente 9 palline nere e 7 bianche si estraggono successivamente 3 palline, rimettendo ogni volta nell’urna la pallina estratta. Qual è la probabilità ceh siano tutte e 3 nere? Che siano tutte e tre bianche? Che siano le prime 2 bianche e la terza nera? Che siano 2 bianche e 1 nera? | ![Rendered by QuickLaTeX.com \left [ \left ( \cfrac{9}{16} \right )^{3}; \left ( \cfrac{7}{16} \right )^{3}; \left ( \cfrac{7}{16} \right )^{2}\cdot \cfrac{9}{16};3\cdot \left ( \cfrac{7}{16} \right )^{2}\cdot \cfrac{9}{16} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a6c16d0173a0bbea4242a130b113f14e_l3.png) |
| Si gettano in aria 2 monete. Qual è la probabilità che diano entrambe testa? Una sola testa? Almeno una testa? | ![Rendered by QuickLaTeX.com \left [ \cfrac{1}{4};\cfrac{1}{2};\cfrac{3}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-500f40a40397a635b810da8f834f7761_l3.png) |
[:it]

Joel Rea
L’ellisse è quel luogo dei punti del piano per cui è costante la somma delle distanze da due punti fissi detti fuochi.
L’ellisse rappresenta ad esempio il percorso dei pianeti attorno al Sole, la forma stessa della Terra è ellittica, un uovo è ellittico, lo stesso cerchione di un pneumatico se non perfettamente rotondo viene rappresentato da un’ellisse.
Come nelle precedenti forme geometriche anche l’ellisse ha un’equazione che la rappresenta.
![]()
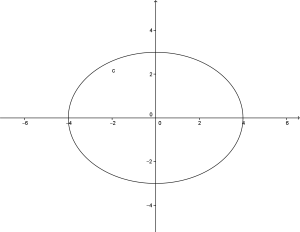
Se due fuochi dell’ellisse hanno coordinate:
![]()
allora ![]()
![]()
e l’ellisse ha questa rappresentazione grafica
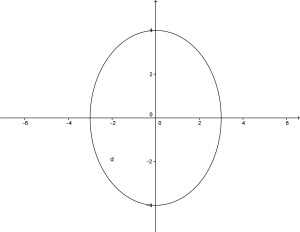
Se invece i due fuochi delle ellisse hanno coordinate:
![]()
allora ![]()
![]()
e l’ellisse ha questa rappresentazione grafica:
 ma la
ma la ![]() e la
e la ![]() cosa rappresentano?
cosa rappresentano?
Danno la lunghezza dei semiassi dell’ellisse.
In pratica l’ellisse è racchiusa in un rettangolo i cui lati sono ![]() e
e ![]() .
.
Ossia si ha una figura del genere:
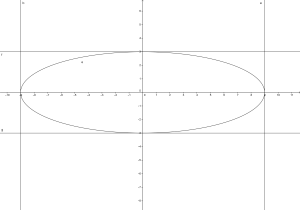 ma cosa differisce un’ellisse da una circonferenza?
ma cosa differisce un’ellisse da una circonferenza?
Dall’eccentricità ossia di quanto essa è schiacciata rispetto o l’asse x o l’asse y.
in pratica l’eccentricità è un rapporto tra la coordinata dei fuochi e l’asse maggiore dell’ellisse.
![]()
Nel caso della circonferenza ![]() per cui
per cui ![]() ed, infatti, l’eccentricità è nulla.[:en]
ed, infatti, l’eccentricità è nulla.[:en]

Joel Rea
L’ellisse è quel luogo dei punti del piano per cui è costante la somma delle distanze da due punti fissi detti fuochi.
L’ellisse rappresenta ad esempio il percorso dei pianeti attorno al Sole, la forma stessa della Terra è ellittica, un uovo è ellittico, lo stesso cerchione di un pneumatico se non perfettamente rotondo viene rappresentato da un’ellisse.
Come nelle precedenti forme geometriche anche l’ellisse ha un’equazione che la rappresenta.
![]()
Se due fuochi dell’ellisse hanno coordinate:
![]()
allora ![]() e l’ellisse ha questa rappresentazione grafica
e l’ellisse ha questa rappresentazione grafica

Se invece i due fuochi delle ellisse hanno coordinate:
![]()
allora ![]()
e l’ellisse ha questa rappresentazione grafica:
 ma la
ma la ![]() e la
e la ![]() cosa rappresentano?
cosa rappresentano?
Danno la lunghezza dei semiassi dell’ellisse.
In pratica l’ellisse è racchiusa in un rettangolo i cui lati sono ![]() e
e ![]() .
.
Ossia si ha una figura del genere:
 ma cosa differisce un’ellisse da una circonferenza?
ma cosa differisce un’ellisse da una circonferenza?
Dall’eccentricità ossi di quanto essa è schiacciata rispetto o l’asse x o l’asse y.
in pratica l’eccentricità è un rapporto tra la coordinata dei fuochi e l’asse maggiore dell’ellisse.
![]()
Nel caso della circonferenza ![]() per cui
per cui ![]() ed, infatti, l’eccentricità è nulla.[:de]
ed, infatti, l’eccentricità è nulla.[:de]
Die Ellipse
Eine Ellipse kann definiert werden als die Menge aller Punkte der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten und gleich einer gegebenen Konstante ist. Die Punkte und heißen Brennpunkte.
Die Ellipse repräsentiert zum Beispiel den Kurs von den Planeten um die Sonne, die gleiche Form von der Erde ist elliptisch, ein Ei ist elliptisch, Felgen von einem Reifen, wenn es nicht genau rund ist spricht man von einer Ellipse.
Wie auch die vorhergehenden geometrischen Formen wird die Ellipse durch eine Gleichung dargestellt.
Wenn zwei Brennpunkte der Ellipse Koordinaten haben,
hat die Ellipse diese grafische Darstellung
Wenn die Brennpunkte hingegen folgende Koordinaten haben,
hat die Ellipse diese grafische Darstellung
aber was stellen a und b dar?
Sie geben die Länge der Halbachsen der Ellipse an.
In der Praxis ist die Ellipse in einem Rechteck enthalten, dessen Seiten 2a und 2b sind.
Oder wir haben eine Form dieser Art:
Aber was unterscheidet eine Ellipse von einem Umfang?
Entweder die Exzentrizität oder wieviel die Ellipse hinsichtlich der Achse x oder y zerquetscht ist.
Die Exzentrizität ist also eine Beziehung zwischen der Koordinate der Brennpunkte und der größten Achse der Ellipse.
Wenn der Umfang a=b bzw. C=0, ist die Exzentrizität null.
[:]