SCIENZE E TECNOLOGIE INFORMATICHE

Esercizi sulle parabole per livelli

Pubblicato il 4 Marzo 2016 da admin

Czlowiek Kamera

Dopo tutti i post di approfondimento sulle equazioni di secondo grado, lo svolgimento passo passo per rappresentare la parabola sul piano cartesiano adesso elenco una serie di esercizi necessari per verificare il proprio grado di comprensione sul tema parabola.

Esercizi di base (6):

Determinare le coordinate del vertice, del fuoco e le equazioni dell’asse di simmetria e della direttrice delle seguenti parabole.

6.1. $y=-x^2+8x-7$	$\left [ V(4,9);F\left ( 4,\cfrac{35}{4} \right );x=4;y=\cfrac{37}{4} \right ]$
6.2. $y=\cfrac{x^2}{4}-1$	$\left [ V(0,-1);F\left ( 0,0 \right );x=0;y=-2 \right ]$
6.3. $y=-x^2-4x+3$	$\left [ V\left(2,-1);F\left ( 2,-\cfrac{3}{4} \right );x=2;y=-\cfrac{5}{4} \right ]$

Esercizi per un livello discreto (7)

Determinare le coordinate del vertice, del fuoco e le equazioni dell’asse di simmetria e della direttrice delle seguenti parabole.

7.1. $y=x^2+x+4$	$\left [ V\left(-\cfrac{1}{2},\cfrac{15}{4}\right);F\left ( -\cfrac{1}{2},4 \right );x=-\cfrac{1}{2};y=\cfrac{7}{2} \right ]$
7.2. $y=x^2-x-12$	$\left [ V\left(\cfrac{1}{2},-\cfrac{49}{4}\right);F\left ( \cfrac{1}{2},-12 \right );x=\cfrac{1}{2};y=-\cfrac{25}{2} \right ]$

Pubblicato in Senza categoria | Lascia un commento

Esercizi sulla fattorizzazione di polinomi

Pubblicato il 4 Marzo 2016 da admin

6.1. $x^2yz + xy^2 + xy$	$\left [ xy(xz + y + 1) \right ]$
6.2. $a^2bx + ab^2y + ax + by$	$[(ab + 1)(ax + by)]$
6.3. $ax^4-ay^4$	$[a(x + y)(x−y)(x^2 + y^2)]$
6.4. $a^2x + 2ax + x + a^2y^2 + 2ay^2 + y^2$	$[(x + y^2)(a + 1)^2]$
6.5. $ax^3-by^3 + bx^3-ay^3$	$[(a + b)(x−y)(x^2 + xy + y^2)]$
6.6. $x^3y + 2x^2y + 2xy + y$	$[ y(x + 1)(x2 + x + 1)]$
6.7. $x^2y^2z^2 + 4x^2y^2z + 3x^2y^2$	$[x^2y^2(z + 1)(z + 3)]$
6.8. $xyz^2 + 10xyz + 25xy$	$[xy(z + 5)^2]$

Pubblicato in Senza categoria | Lascia un commento

Scomposizione (fattorizzazione dei polinomi)

Pubblicato il 3 Marzo 2016 da admin

O-Que-e-Surrealismo-Metodo-Paranoico-critico Tale post nasce dall’esigenza di poter apprendere cosa significa la fattorizzazione di polinomi.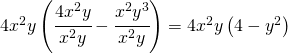

La fattorizzazione è la determinazione del massimo comune denominatore tra i monomi componenti un polinomio.

E’ indispensabile conoscerla per capire successivamente come poter sviluppare le equazioni frazionarie, le espressioni frazionarie e molti studi di funzione che si affrontano nel percorso di approfondimento di matematica.

Con un primo esempio spero di chiarie il problema posto.

Dato il polinomio

$4x^2y-x^2y^3$

si nota che il M.C.D, ossia i termini comuni tra i due monomi, è $x^2y$ .

Quindi lo raccolgo e diventa:

$4x^2y\left ( \cfrac{4x^2y}{x^2y}-\cfrac{x^2y^3}{x^2y} \right )=4x^2y\left ( 4-y^2 \right )$

Adesso ricordandomi la differenza del quadrato di un binomio (prodotti notevoli) l’espressione precedente risulta:

$4x^2y\left ( 4-y^2 \right )=4x^2y\left ( 2-y \right )\left ( 2+y \right )$ .

Pubblicato in Senza categoria | Lascia un commento

Triangolo

Pubblicato il 28 Febbraio 2016 da admin

Jim Warren

Il triangolo è una tra le figure più studiate e che necessitano di maggiori elementi che lo caratterizzano.

Si distinguono infatti tre triangoli:

triangolo scaleno
- ha i tre lati diversi
triangolo isoscele
- ha due lati uguali e i due angoli alla base uguali
triangolo rettangolo
- ha un angolo di 90°
- i lati che formano l’angolo di 90° si chiamano cateti ed il terzo ipotenusa

Si definiscono poi tre segmenti fondamentali

mediana: congiunge un vertice al punto medio (il punto che divide in due un lato) del lato opposto. Il punto di incrocio delle mediane si chiama baricentro. Si noti poi che il baricentro è il centro di massa ossia se voglio mantenere in equilibrio una figura piana devo trovare il baricentro.

Mediana e baricentro

bisettrice: è il segmento che divide un angolo in due parti uguali. Il punto d’incontro si chiama incentro. La proprietà dell’incentro di un triangolo è che coincide con la circonferenza inscritta al triangolo. Una circonferenza è inscritta quando è tangente ai lati del triangolo.

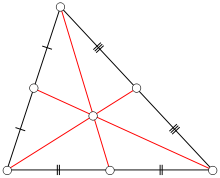
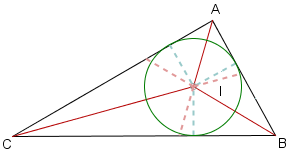
Bisettrice – incentro- circonferenza inscritta

asse: è il segmento che passa per il punto medio di un lato ed è ad esso perpendicolare. Il punto d’incontro si chiama circocentro. La proprietà del circocentro è quello che coincide con il centro della circonferenza che circoscrive il triangolo.

Assi – Circocentro – circonferenza circoscritta

Pubblicato in Senza categoria | Lascia un commento

Teorema di Pitagora

Pubblicato il 28 Febbraio 2016 da admin

Hermin Abramovitch

Il teorema di Pitagora si applica SOLO per i triangoli rettangoli:

Il quadrato costruito sull’ipotenusa è uguale al quadrato costruito sui cateti.

in altri termini l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.

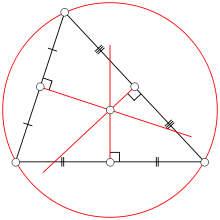
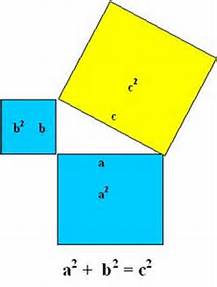thSPYAPPHT Le sue applicazioni sono infinite in quanto data una figura di qualsiasi forma posso sempre trovare al suo interno un triangolo rettangolo.

Le formule che si applicano sono le seguenti:

$i^{2}=c_{1}^{2}+c_{2}^{2}$

dove con

$c_{1}$ e $c_{2}$ si indicano i cateti ossia i due lati che formano tra di loro 90° mentre con la lettera $i$ si indica l’ipotenusa ossia il lato che unisce gli estremi dei due cateti.

dalla formula precedente ricavo

l’ipotenusa dati i due cateti
un cateto dato l’altro cateto e l’ipotenusa

$i=\sqrt{c_{1}^{2}+c_{2}^{2}}$

$c_{1}^{2}=\sqrt{i^2-c_{2}^{2}}$

$c_{2}^{2}=\sqrt{i^2-c_{1}^{2}}$

Pubblicato in Senza categoria | Lascia un commento

Disequazioni frazionarie: introduzione teorica

Pubblicato il 28 Febbraio 2016 da admin

Igor Morski

Le disequazioni frazionarie sono indispensabili quando si tratta il segno di funzioni frazionarie. Esse sono utilizzate in molti campi a partire da quello economico come in quello della fisica.

Eccone un esempio:

$\cfrac{x-1}{x-2}>0$

Per risolverla si deve:

studiare il segno del numeratore
studiare il segno del denominatore
rappresentare le soluzione sulla stessa retta orientata
vedere il segno complessivo effettuando il prodotto.

NOTA importante:

nelle disequazioni frazionarie si studia sempre il numeratore maggiore o uguale a zero, il denominatore maggiore o uguale a zero e poi si considera il segno complessivo confrontandolo con il verso della disequazione di partenza.

Per capire il protocollo precedente sviluppo l’esercizio di partenza.

studio il numeratore

$x-1>0$

$x>1$

studio il denominatore

$x-2>0$

$x>2$

Li rappresento sulla retta orientata

Studio la soluzione:

A destra del due ho una linea continua che significa che tutti i numeri a destra soddisfano il segno di maggiore.

A sinistra invece ho una linea tratteggiata che mi indica che tali numeri mi indicano che la disequazione è negativa.

Adesso noto che – per – fa più ossia in tale zona l’equazione frazionaria è positiva;

La soluzione diventa:

$\left [ x<1,x>2 \right ]$

Pubblicato in Senza categoria | Lascia un commento

Portare dentro al segno di radice

Pubblicato il 26 Febbraio 2016 da admin

[:it]

Igor Morski

Utilizzando la proprietà che:

$\sqrt[n]{a^{n}}=a$

posso portare sotto il segno di radice qualunque cifra.

Quindi devo elevare il numero che voglio portare sotto il segno di radice all0 stesso indice della radice per poi mettere il numero e il resto della radicando sotto la stessa radice.

Spero con un esempio di chiarire la cosa.

$5\cdot \sqrt[3]{2}=\sqrt[3]{5^{3}}\cdot \sqrt[3]{2}=\sqrt[3]{5^3\cdot 2}=\sqrt[3]{125\cdot 2}=\sqrt[3]{250}$

Esercizi[:en]

Igor Morski

Utilizzando la proprietà che:

$\sqrt[n]{a^{n}}=a$

posso portare sotto il segno di radice qualunque cifra.

Quindi devo elevare il numero che voglio portare sotto il segno di radice all0 stesso indice della radice per poi mettere il numero e il resto della radicando sotto la stessa radice.

Spero con un esempio di chiarire la cosa.

$5\cdot \sqrt[3]{2}=\sqrt[3]{5^{3}}\cdot \sqrt[3]{2}=\sqrt[3]{5^3\cdot 2}=\sqrt[3]{125\cdot 2}=\sqrt[3]{250}$

[:de]

Igor Morski

Utilizzando la proprietà che:

$\sqrt[n]{a^{n}}=a$

posso portare sotto il segno di radice qualunque cifra.

Quindi devo elevare il numero che voglio portare sotto il segno di radice all0 stesso indice della radice per poi mettere il numero e il resto della radicando sotto la stessa radice.

Spero con un esempio di chiarire la cosa.

$5\cdot \sqrt[3]{2}=\sqrt[3]{5^{3}}\cdot \sqrt[3]{2}=\sqrt[3]{5^3\cdot 2}=\sqrt[3]{125\cdot 2}=\sqrt[3]{250}$

[:]

Pubblicato in Senza categoria | Lascia un commento

Portare fuori dal segno di radice

Pubblicato il 26 Febbraio 2016 da admin

Jacek Yerka

La prima cosa è effettuare la scomposizione del numero posto all’interno della radice, poi lo si scompone in maniera tale da avere l’esponente del radicando uguale all’indice della radice in maniera poi da portare fuori dal segno di radice il numero stesso.

Con un esempio spero di chiarire la cosa.

Calcolare:

$\sqrt{8}$

scompongo l’8:

$\begin{matrix} 8 &| &2 \\ 4 &| &2 \\ 2 &| &2\\ 1 &&\\ \end{Matrix}$

ossia $8=2^3=2^2 \cdot 2$

$\sqrt{8}=\sqrt[2]{8}=\sqrt[2]{2^3}=\sqrt[2]{2^2\cdot 2}=\sqrt[2]{2^2}\cdot \sqrt[2]{2}=\sqrt[\not{2}]{2^{\not{2}}}\cdot \sqrt[2]{2}=2\cdot \sqrt[2]{2}$

Pubblicato in Senza categoria | Lascia un commento

Esercizi sul punto medio di un segmento

Pubblicato il 26 Febbraio 2016 da admin

Kevin Corrado

Per sviluppare questi esercizi consiglio di leggere il post sul punto medio di un segmento

Determina il punto medio del segmento AB, di estremi A e B.

La difficoltà è indicata con la cifra progressiva con 6 il più immediato e 10 il più complesso.

6.1. $A\left ( -1,2 \right ),B\left ( 3,4 \right )$	$\left [ \left ( 1,3 \right ) \right ]$
6.2. $A\left ( -1,0 \right ),B\left ( -4,0 \right )$	$\left [ \left ( -\cfrac{5}{2},0 \right ) \right ]$
6.3. $A\left ( 1,-8 \right ),B\left ( 1,-3 \right )$	$\left [ \left (1,-\cfrac{11}{2} \right ) \right ]$
6.4. $A\left ( 2,-1 \right ),B\left (- 1,2 \right )$	$\left [ \left (\cfrac{1}{2},\cfrac{1}{2} \right ) \right ]$
6.5. $A\left ( 3,-2 \right ),B\left ( -1,-2 \right )$	$\left [ \left ( 1,-2 \right ) \right ]$
6.6. $A\left (-2,1 \right ),B\left ( 4,5 \right )$	$\left [ \left ( 1,3 \right ) \right ]$
7.1. $A\left ( 1-\sqrt{3},4 \right ),B\left ( 1+\sqrt{3},6 \right )$	$\left [ \left ( 1,5 \right ) \right ]$
7.2. $A\left ( -\sqrt{5},-\sqrt{3} \right ),B\left ( \sqrt{5},3\sqrt{3} \right )$	$\left [ \left (0,\sqrt{3} \right ) \right ]$

Pubblicato in Senza categoria | Lascia un commento

Punto medio di un segmento

Pubblicato il 26 Febbraio 2016 da admin

Kevin Corrado

Siano $A(x_{1},y_{1})$ e $B(x_{2},y_{2})$ due punti del piano cartesiano e M il punto medio (è quel punto che divide in due parti uguali) del segmento AB.

L’ascissa di M è la media aritmetica delle ascisse di A e B e l’ordinata di M è la media aritmetica delle ordinate di A e B; in simboli

$M\left ( \cfrac{x_{1}+x_{2}}{2},\cfrac{y_{1}+y_{2}}{2} \right )$

ESEMPIO

Determinare il punto medio del segmento di estremi $A\left ( -2,3 \right )$ e $B\left ( 4,-1 \right )$ .

Meglio sempre scrivere:

$x_{1}=-2,y_{1}=3$

$x_{2}=4,y_{2}=-1$

Applicando la definizione precedente il punto medio risulta:

$x_{M}=\cfrac{-2+4}{2}=1$

$y_{M}=\cfrac{3-1}{2}=1$

$M\left ( 1,1 \right )$

Per esercitarsi

Pubblicato in Senza categoria | Lascia un commento

Esercizi sulle parabole per livelli

Esercizi sulla fattorizzazione di polinomi

Scomposizione (fattorizzazione dei polinomi)

Triangolo

Teorema di Pitagora

Disequazioni frazionarie: introduzione teorica

Portare dentro al segno di radice

Portare fuori dal segno di radice

Esercizi sul punto medio di un segmento

Punto medio di un segmento

Registrazione

Categorie

Articoli recenti

Commenti recenti

Meta

Categorie

Articoli recenti

Commenti recenti

Meta

Whymatematica