
Jim Warren
Descrivere un insieme di cose in maniera sintetica è una caratteristica spontanea dell’uomo: quante sono le macchine rosse, quanti uomini o donne vi sono in un gruppo, quante sono le materie in un anno scolastico, com’è il rendimento scolastico.
Ad esempio se voglio una descrizione della tipologia di persone che frequentano un ristorante, ho bisogno di strumenti affinché possa poi capire che tipo di cucina o che alimenti debba comprare.
Cerco di partire da un esempio: i voti presi durante un anno scolastico.
6, 5, 4, 6, 7,6,5,
Il primo parametro è la frequenza.
Si definisce frequenza assoluta il numero di volte che quel particolare evento si ripete.
Nel caso dell’esempio precedente ho:
| Evento | frequenza assoluta |
| 6 | 3 |
| 5 | 2 |
| 4 | 1 |
| 7 | 1 |
| Totale | 7 |
La frequenza relativa invece è la frequenza assoluta espressa in percentuale rispetto al totale dell’evento.
| evento | frequenza assoluta | frequenza relativa |
| 6 | 3 | |
| 5 | 2 | |
| 4 | 1 | |
| 7 | 1 | |
| totale | 7 | 100% |
Conoscere la frequenza con cui un evento si ripete è fondamentale per far fronte a quell’evento più probabile in maniera migliore. Ad esempio se la frequenza dei clienti che chiedono una pizza margherita è superiore a quella di coloro che chiedono una pizza alla verdure dovrò acquistare meno verdure.


![Rendered by QuickLaTeX.com \left[\cfrac{7}{x+2}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-54046183c8ce402bd873f3fe1da73dcd_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{6x}{x+2y}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-25e15a79e3953112dfde74a771ae9a83_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{2a}{a+1}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-87dc784053b1a3af04255d5559c124c5_l3.png)
![Rendered by QuickLaTeX.com \left[\cfrac{1-x}{a-x^2}\right]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3191b1f9c9d953f51225a43cc7645b1_l3.png)

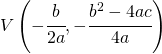
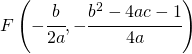
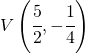
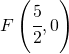



![Rendered by QuickLaTeX.com \left [ V(4,9);F\left ( 4,\cfrac{35}{4} \right );x=4;y=\cfrac{37}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a614de79c7aeedeb51cb06dedd8977e2_l3.png)
![Rendered by QuickLaTeX.com \left [ V\left(2,-1);F\left ( 2,-\cfrac{3}{4} \right );x=2;y=-\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a5a85a831806c3dd5a95a091f775ed45_l3.png)
![Rendered by QuickLaTeX.com \left [ V\left(-\cfrac{1}{2},\cfrac{15}{4}\right);F\left ( -\cfrac{1}{2},4 \right );x=-\cfrac{1}{2};y=\cfrac{7}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-933879babdba32e43bfc377c8bf3889e_l3.png)
![Rendered by QuickLaTeX.com \left [ V\left(\cfrac{1}{2},-\cfrac{49}{4}\right);F\left ( \cfrac{1}{2},-12 \right );x=\cfrac{1}{2};y=-\cfrac{25}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e068f3d66c9ac19e0592dcb41442d698_l3.png)
 Tale post nasce dall’esigenza di poter apprendere cosa significa la fattorizzazione di polinomi.
Tale post nasce dall’esigenza di poter apprendere cosa significa la fattorizzazione di polinomi.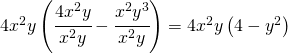

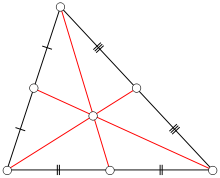
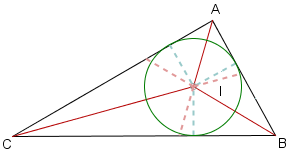

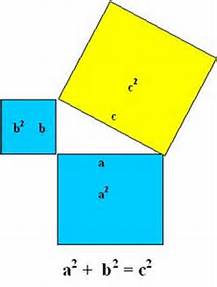 Le sue applicazioni sono infinite in quanto data una figura di qualsiasi forma posso sempre trovare al suo interno un triangolo rettangolo.
Le sue applicazioni sono infinite in quanto data una figura di qualsiasi forma posso sempre trovare al suo interno un triangolo rettangolo.
 Studio la soluzione:
Studio la soluzione: