 Le disequazioni di secondo grado possono essere risolte o applicando la scomposizione del polinomio di secondo grado o attraverso il metodo grafico o della parabola.
Le disequazioni di secondo grado possono essere risolte o applicando la scomposizione del polinomio di secondo grado o attraverso il metodo grafico o della parabola.
Scomposizione del polinomio di secondo grado
un polinomio di secondo grado può sempre essere scritto come:
![]()
dove
![]()
sono le soluzioni dell’equazione
![]()
quindi si studia il grafico per determinare il segno finale della disequazione:
![]()
o della disequazione:
![]()
Unica avvertenza studiare SEMPRE
![]()
e
![]()
ed il segno di a
Con questi esempi spero di chiarire la cosa:
Es1.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=1
Studio il segno di
![]()
![]()
Rappresento graficamente la soluzione evidenziando che essendo un prodotto verifico dove il prodotto fornisce il segno positivo.
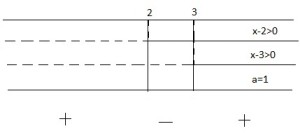 Si noti che la a=1 e quindi la si rappresenta con una linea continua.
Si noti che la a=1 e quindi la si rappresenta con una linea continua.
La soluzione è
![]()
Es2.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=1
Studio il segno di
![]()
![]()
Si NOTA che si studia comunque il segno maggiore di zero!
Rappresento graficamente la soluzione evidenziando che essendo un prodotto verifico dove il prodotto fornisce il segno Negativo questa volta

La soluzione, questa volta è:
![]()
Es3.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=-1
Studio il segno di
![]()
![]()
Rappresento graficamente la soluzione evidenziando che essendo un prodotto verifico dove il prodotto fornisce il segno positivo
Si noti che questa volta la a=-1 ossia viene rappresentata con una linea tratteggiata.
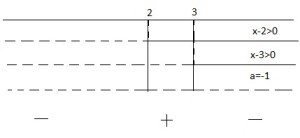 devo studiare dove si ha il segno positivo ed è tra 2 e 3.
devo studiare dove si ha il segno positivo ed è tra 2 e 3.
![]()
Metodo grafico
Il metodo grafico è molto semplice, è sufficiente conoscere la rappresentazione di una parabola e le sue intersezioni con l’asse delle x che sono le soluzioni della relativa equazione di secondo grado.
Es1.
![]()
risolvo l’equazione:
![]()
essa ha soluzione:
![]()
e la
a=1
la rappresentazione sul piano cartesiano è:
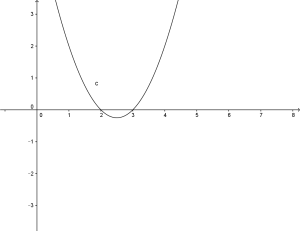
Si noti subito che la parabola è sopra l’asse delle x per quei valori per cui:
![]() .
.
Es2.
Nel secondo esempio si deve studiare:
![]()
Il procedimento è uguale all’esempio precedente ed il grafico pure:
 ma questa volta si vuole saper dov’è minore di zero:
ma questa volta si vuole saper dov’è minore di zero:
![]() .
.
Es3.
![]()
in questo caso le soluzioni sono sempre le stesse ma il grafico è:
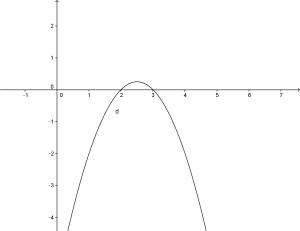 e dov’è maggiore di zero?
e dov’è maggiore di zero?
![]()


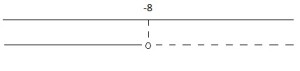 6.2.
6.2.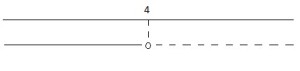
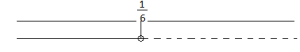 7.2.
7.2. 8.1.
8.1.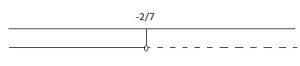

![Rendered by QuickLaTeX.com \left [ x_{m}=1; x_{M}=\cfrac{1}{3}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-993517ae371a224c88dd10074138148a_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=-\cfrac{1}{\sqrt[3]{2}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b7df9977da9b101a8e89ca0c48d0424f_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=\cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ff79fc4452acaf2aeab4d08def37c25a_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=\cfrac{3}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9739cef6049e9391026d1f9c9cf5cdf8_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=0;x_{m}=\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-696f940d5d38852351e620444e840174_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=\cfrac{7}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5e9fc2daa5d346872f3eccd8b498075a_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=\cfrac{1}{e} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-10f740d6b72e4057d6584693169797fd_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=\cfrac{1}{\sqrt{e}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1e80a39b864fffd12539bcea527e4815_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=0-;x_{M}=\cfrac{8}{27} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e634c80386c87b70db89ba35e58b76b1_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=-1;x_{m}=-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e005ac5af3526c142ebdc7f30c8a421c_l3.png)

![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-34bc2ff7aead278c493a9716fe841b55_l3.png)
![Rendered by QuickLaTeX.com \left [ x> \cfrac{5}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-90c121580c491dbfbf8f050df9602243_l3.png)
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-410949a150ffd3eb758a161cc340088d_l3.png)
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{1}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-880015ba231003b8163ca46a376d0f66_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-88d4b62eabf58f96bdc307163bc733d8_l3.png)
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{5}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d3a0c1c33cde37730ec2bd521f999d0c_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{7}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc0b925830708c1a3f142d9e97681614_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{4}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9c09fec77f628e93139e0abf1734aa_l3.png)
![Rendered by QuickLaTeX.com \left [x<\cfrac{1}{6}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2a63066896d443b89558d1f9aefb3d83_l3.png)
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2de43c2738ee6f1ab07ce36e9153b791_l3.png)
![Rendered by QuickLaTeX.com \cfrac{1}{5}\left ( x-2 \right )-\left [ 1+2x-\left ( x+\cfrac{1}{2} \right ) \right ]\leq 1](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-36f4af288d2c0cf8680b77c48afe0de9_l3.png)
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{19}{8} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5b393050de4f374b692e0a9f794b77f9_l3.png)
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{2}{7} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ccf45ccc6650a4b66a098051b4794f60_l3.png)
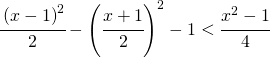
![Rendered by QuickLaTeX.com 9x+20\geq 2\left [ \cfrac{29}{4}-6\left ( x-1 \right )+9x-\cfrac{9}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-60c738380ef84b193542335c382f0b8b_l3.png)
![Rendered by QuickLaTeX.com \left [ x\geq \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6c1e262716e69477c58bbb99e19158af_l3.png)
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{4}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-233dc8229b397df8faadec86bc3d1bf5_l3.png)
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png)

 Ossia si consideri che:
Ossia si consideri che: [WpProQuiz 16]
[WpProQuiz 16] [WpProQuiz 10]
[WpProQuiz 10] [WpProQuiz 15]
[WpProQuiz 15]
 [WpProQuiz 13]
[WpProQuiz 13]