 6.1.1. Data la seguente equazione
6.1.1. Data la seguente equazione 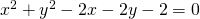 posso identificare
posso identificare 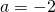 ,
, 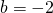 e
e 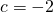 .
.
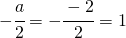
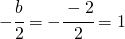
quindi il centro ha equazione:
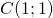
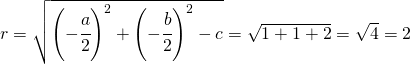
A questo punto per rappresentare la circonferenza sul piano cartesiano fisso prima il centro e poi posso usare il raggio.
Posso inoltre determinare le intersezioni con gli assi impostando i seguenti due sistemi:
Per le intersezioni con l’asse delle y
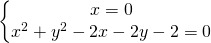
Per le intersezioni con l’asse delle x
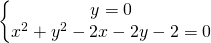
il primo sistema comporta il risolvere l’equazione:
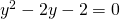
(equazioni di secondo grado) le cui soluzioni sono:
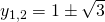
il secondo sistema comporta il risolvere l’equazione:
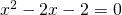
le cui soluzioni sono:
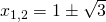
Il grafico risulta quindi:
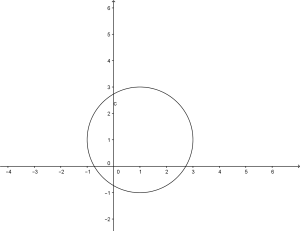
6.2.1. Dati 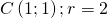 trovare l’equazione della circonferenza.
trovare l’equazione della circonferenza.
Si parte questa volta da questa forma della circonferenza:
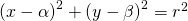
in cui 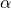 e
e 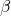 sono le coordinate del centro ed
sono le coordinate del centro ed  è il valore del raggio.
è il valore del raggio.
Sostituendo quindi i dati del problema si ha:
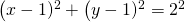
sviluppando i prodotti notevoli ho:
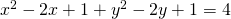
riordino l’equazione:
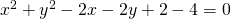
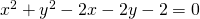
che è la richiesta del problema
7.3.
Dato il centro ed un punto 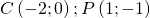 per determinare l’equazione della circonferenza calcolo la distanza tra il centro C ed il punto P che rappresenta il raggio.
per determinare l’equazione della circonferenza calcolo la distanza tra il centro C ed il punto P che rappresenta il raggio.
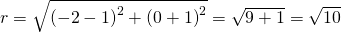
Adesso utilizzo la formula dato il centro ed il raggio che applicata diventa:
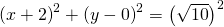
sviluppo le parentesi:
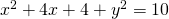
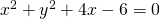
8.1. Equazione della circonferenza di diametro A e B.
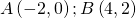
il punto medio è il centro della circonferenza e quindi risulta:
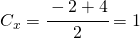
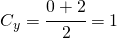
quindi il centro risulta:
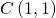
Adesso calcolo la distanza tra A e B ed il risultato lo divido per 2 e trovo il raggio.
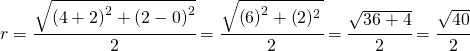
Adesso uso la formula che permette di ricavare l’equazione della circonferenza dato il centro ed il raggio.
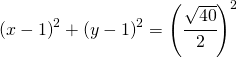
sviluppo le parentesi ed ho:
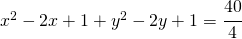
ordino i termini e sommo quelli simili:
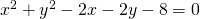
9.1. Dati i seguenti tre punti calcolare l’equazione della circonferenza.
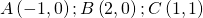
Si deve partire dal fatto che per verificare che un punto appartenga ad una funzione deve valere l’identità ossia se sostituisco le coordinate di un punto nell’equazione generica della circonferenza 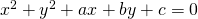 devo trovare un’identità.
devo trovare un’identità.
Sostituisco le coordinate di A:
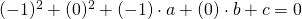
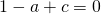
Sostituisco le coordinate di B:
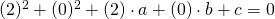
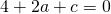
Sostituisco le coordinate di C:
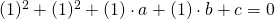
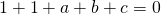
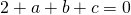
Ho tre equazioni in tre incognite e devo saper risolvere un sistema a tre equazioni in tre incognite.
Se si dovesse avere difficoltà nel risolvere il sistema d’equazioni andare a rivedersi il post:
sistemi d’equazione metodo della sostituzione
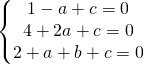
utilizzo appunto il metodo della sostituzione andando a sostituire il valore di c nella seconda e nella terza equazione.
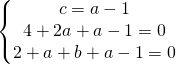
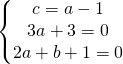
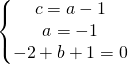
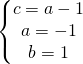
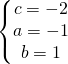
Adesso sostituisco i valori trovati nell’equazione generica della circonferenza:
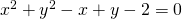
che è il risultato voluto.

![]() e
e ![]() due punti del piano cartesiano e M il punto medio (è quel punto che divide in due parti uguali) del segmento AB.
due punti del piano cartesiano e M il punto medio (è quel punto che divide in due parti uguali) del segmento AB.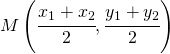
![]() e
e ![]() .
.![]()
![]()
![]()
![]()
![]()


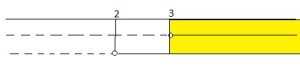 e la soluzione è
e la soluzione è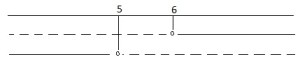 e si nota che la linea continua non si sovrappone mai per cui la soluzione è l’insieme vuoto e si indica appunto:
e si nota che la linea continua non si sovrappone mai per cui la soluzione è l’insieme vuoto e si indica appunto: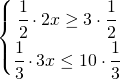
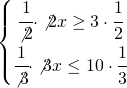
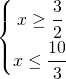
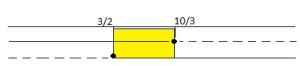 e si nota che la soluzione è compresa tra le due frazioni e si scrive:
e si nota che la soluzione è compresa tra le due frazioni e si scrive: risolvere i sistemi di disequazione è sufficiente essere in grado di risolvere le disequazioni lineari e ricordarsi che la soluzione viene data dalla regione in cui entrambe contemporaneamente risolvono le rispettive disequazioni di partenza.
risolvere i sistemi di disequazione è sufficiente essere in grado di risolvere le disequazioni lineari e ricordarsi che la soluzione viene data dalla regione in cui entrambe contemporaneamente risolvono le rispettive disequazioni di partenza.![Rendered by QuickLaTeX.com \left [ \cfrac{3}{2}\leq x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d874d6865e9738e5a0e0a8e1ee9670d1_l3.png)
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png)
![Rendered by QuickLaTeX.com \left [ \cfrac{5}{2}\leq x<\cfrac{7}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc102b92e782701a3973533343d93ee5_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e63eca605efe9170d16822b5d0d2adf2_l3.png)
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{1}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5a3e5d51b7e2a1b42cdda69308d34417_l3.png)
![Rendered by QuickLaTeX.com \left [ -\cfrac{4}{3}<x<\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-72e747f7aabf492ce7c0ef9261028634_l3.png)
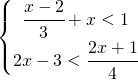
![Rendered by QuickLaTeX.com \left [ x<\cfrac{5}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-96dbd5e87d5edb2f6469946aaa0fb7dc_l3.png)
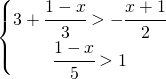
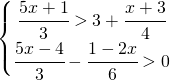
![Rendered by QuickLaTeX.com \left [ x>\cfrac{41}{17}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e549ca2ccebdcab7ea6766e9bb3a5cec_l3.png)
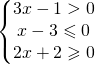 .
.![Rendered by QuickLaTeX.com \left [ \cfrac{1}{3}<x\leqslant 3 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-aee70d4e862ad2e7591477f51a8e5b60_l3.png)
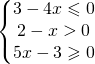
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{4}\leqslant x<2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-be87c42e4e2f223068cd48943fa66bbe_l3.png)
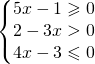
![Rendered by QuickLaTeX.com \left [ \cfrac{1}{5}\leqslant x< \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d7a4db19a611fb5dcfefdafcdf341945_l3.png)
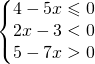
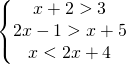
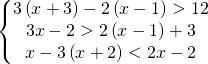
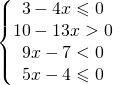
![Rendered by QuickLaTeX.com \left [ \cfrac{3}{4}\leqslant x<\frac{10}{13} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79634375285228736576b033de4b9385_l3.png)
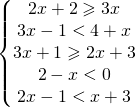
 Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado.
Tutti i seguenti quiz possono essere affrontati dopo aver compreso come effettuare le derivate, conoscere le disequazioni e le equazioni di primo e secondo grado. La probabilità di un evento è la misura del grado di fiducia che una persona ha nel verificarsi dell’evento.
La probabilità di un evento è la misura del grado di fiducia che una persona ha nel verificarsi dell’evento. Data la seguente equazione frazionaria:
Data la seguente equazione frazionaria: Il metodo di Cramer lo applico al seguente sistema:
Il metodo di Cramer lo applico al seguente sistema: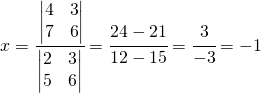
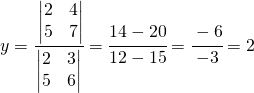
 Questo metodo presuppone la conoscenza di una nuova operazione che si chiama determinante.
Questo metodo presuppone la conoscenza di una nuova operazione che si chiama determinante. 6.1.1. Data la seguente equazione
6.1.1. Data la seguente equazione 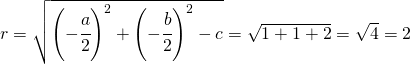

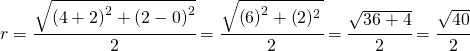
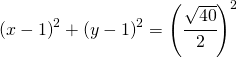
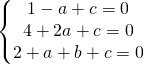
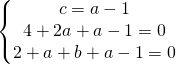
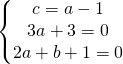
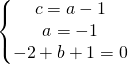
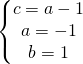
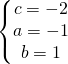
 Gli esercizi sulla circonferenza sono normalmente di questo tipo:
Gli esercizi sulla circonferenza sono normalmente di questo tipo:![Rendered by QuickLaTeX.com \left [ C\left ( 1;\cfrac{1}{2} \right );r=\cfrac{\sqrt{3}}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2241daf9b8fb29c1389d640b1a9095f2_l3.png)
![Rendered by QuickLaTeX.com \left [ C\left ( \cfrac{1}{2};1 \right );r=2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2d6b347a7a547e6cbe792851e0df679e_l3.png)