 Gli esercizi sulla circonferenza sono normalmente di questo tipo:
Gli esercizi sulla circonferenza sono normalmente di questo tipo:
- data l’equazione della circonferenza determinare il centro ed il raggio e farne la sua rappresentazione sul piano cartesiano con le relative intersezioni.
- dato il centro ed un punto appartenente alla circonferenza, trovare l’equazione della circonferenza
- dati tre punti appartenenti alla circonferenza trovare la relativa equazione
- data una retta ed una circonferenza, stabilire la loro posizione reciproca
- dato un punto trovare la retta passante per questo punto e tangente alla circonferenza
Esercizi elementari (6) di tipo 1: determinazione centro e raggio e relativo disegno
| 6.1.1. |
|
| 6.1.2 |
|
| 6.1.3. |
|
| 6.1.4. |
|
| 6.1.5. |
Esercizi elementari (6) di tipo 2: determinazione dell’equazione della circonferenza dato il centro ed il raggio
| 6.2.1. |
|
| 6.2.2. |
Esercizi per un livello discreto (7): determinazione centro e raggio e rappresentazione sul piano cartesiano
| 7.1. |
![Rendered by QuickLaTeX.com \left [ C\left ( 1;\cfrac{1}{2} \right );r=\cfrac{\sqrt{3}}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2241daf9b8fb29c1389d640b1a9095f2_l3.png) |
| 7.2. |
![Rendered by QuickLaTeX.com \left [ C\left ( \cfrac{1}{2};1 \right );r=2 \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2d6b347a7a547e6cbe792851e0df679e_l3.png) |
Determinare l’equazione della circonferenza che ha centro in C e passa per P, e rappresentala graficamente.
Per sviluppare tali esercizi è necessario conoscere la distanza tra due punti
| 7.3. |
|
| 7.4. |
|
| 7.5 |
|
| 7.6. |
|
| 7.7. |
Per essere in grado di sviluppare questi esercizi è necessario conoscere come calcolare il punto medio di un segmento.
Esercizi per un buon livello (8): scrivi l’equazione delle circonferenze di diametro AB e rappresentale sul piano
| 8.1. |
|
| 8.2. |
|
| 8.3. |
|
| 8.4. |
|
| 8.5. |
Esercizi per un livello che dimostra una certa sicurezza nell’operare (9-10).
Quello che serve conoscere è la condizione di appartenenza di un punto ad una funzione e sape risolvere un sistema di tre equazioni in tre incognite.
Scrivi l’equazione della circonferenza passante per i punti A, B, C e rappresentala graficamente.
| 9.1. |
|
| 9.2. |
|
| 9.3. |
|
| 9.4. |
|
| 9.5. |
|
| 9.6. |
|
Questi esercizi sono utili per verificare la capacità di saper risolvere un sistema d’equazione.
Per avere un’ottima manualità (10)
Determinare la posizione reciproca della retta e della circonferenza e determinare gli eventuali punti d’intersezione
| 10.1 |
|
| 10.2. |
|
| 10.3. |
|
| 10.4. |
|
| 10.5. |
|
| 10.6. |
Problemi che mettono in evidenza le competenze:
C1. Scrivi l’equazione della circonferenza che ha centro in (-1;3) ed è tangente all’asse y.
![]()
C2. Determina l’equazione della circonferenza ce ha centro nell’origine ed è tangente alla retta di equazione ![]()
![]()
C3. Scrivi l’equazione della circonferenza avente il centro di ordinata uguale a 3 e passante per i punti A(8;9) e B(12;1).
![]()


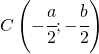
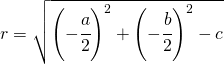

 Le disequazioni di secondo grado possono essere risolte o applicando la scomposizione del polinomio di secondo grado o attraverso il metodo grafico o della parabola.
Le disequazioni di secondo grado possono essere risolte o applicando la scomposizione del polinomio di secondo grado o attraverso il metodo grafico o della parabola.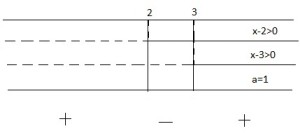 Si noti che la a=1 e quindi la si rappresenta con una linea continua.
Si noti che la a=1 e quindi la si rappresenta con una linea continua.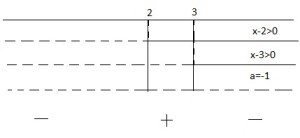 devo studiare dove si ha il segno positivo ed è tra 2 e 3.
devo studiare dove si ha il segno positivo ed è tra 2 e 3.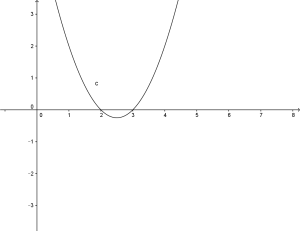
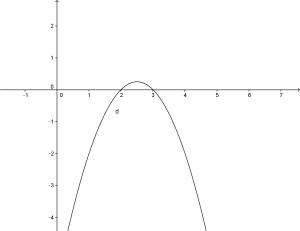 e dov’è maggiore di zero?
e dov’è maggiore di zero?
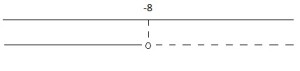 6.2.
6.2.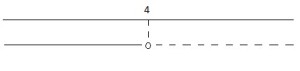
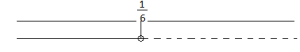 7.2.
7.2. 8.1.
8.1.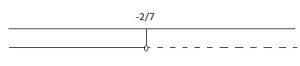

![Rendered by QuickLaTeX.com \left [ x_{m}=1; x_{M}=\cfrac{1}{3}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-993517ae371a224c88dd10074138148a_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=-\cfrac{1}{\sqrt[3]{2}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-b7df9977da9b101a8e89ca0c48d0424f_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=\cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ff79fc4452acaf2aeab4d08def37c25a_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=\cfrac{3}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9739cef6049e9391026d1f9c9cf5cdf8_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=0;x_{m}=\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-696f940d5d38852351e620444e840174_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=\cfrac{7}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5e9fc2daa5d346872f3eccd8b498075a_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=\cfrac{1}{e} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-10f740d6b72e4057d6584693169797fd_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=\cfrac{1}{\sqrt{e}} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-1e80a39b864fffd12539bcea527e4815_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{m}=0-;x_{M}=\cfrac{8}{27} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e634c80386c87b70db89ba35e58b76b1_l3.png)
![Rendered by QuickLaTeX.com \left [ x_{M}=-1;x_{m}=-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e005ac5af3526c142ebdc7f30c8a421c_l3.png)

![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-34bc2ff7aead278c493a9716fe841b55_l3.png)
![Rendered by QuickLaTeX.com \left [ x> \cfrac{5}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-90c121580c491dbfbf8f050df9602243_l3.png)
![Rendered by QuickLaTeX.com \left [ x\leq \cfrac{10}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-410949a150ffd3eb758a161cc340088d_l3.png)
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{1}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-880015ba231003b8163ca46a376d0f66_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{8}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-88d4b62eabf58f96bdc307163bc733d8_l3.png)
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{5}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d3a0c1c33cde37730ec2bd521f999d0c_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{7}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-cc0b925830708c1a3f142d9e97681614_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{2}{9} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7d0d36a6cfb1dbb3430a7f7d20c8829c_l3.png)
![Rendered by QuickLaTeX.com \left [ x>\cfrac{4}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9c09fec77f628e93139e0abf1734aa_l3.png)
![Rendered by QuickLaTeX.com \left [x<\cfrac{1}{6}\right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2a63066896d443b89558d1f9aefb3d83_l3.png)
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-2de43c2738ee6f1ab07ce36e9153b791_l3.png)
![Rendered by QuickLaTeX.com \cfrac{1}{5}\left ( x-2 \right )-\left [ 1+2x-\left ( x+\cfrac{1}{2} \right ) \right ]\leq 1](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-36f4af288d2c0cf8680b77c48afe0de9_l3.png)
![Rendered by QuickLaTeX.com \left [ x\geq -\cfrac{19}{8} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5b393050de4f374b692e0a9f794b77f9_l3.png)
![Rendered by QuickLaTeX.com \left [ x<-\cfrac{2}{7} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ccf45ccc6650a4b66a098051b4794f60_l3.png)
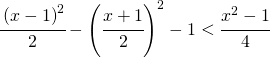
![Rendered by QuickLaTeX.com 9x+20\geq 2\left [ \cfrac{29}{4}-6\left ( x-1 \right )+9x-\cfrac{9}{4} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-60c738380ef84b193542335c382f0b8b_l3.png)
![Rendered by QuickLaTeX.com \left [ x\geq \cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6c1e262716e69477c58bbb99e19158af_l3.png)
![Rendered by QuickLaTeX.com \left [ x>-\cfrac{4}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-233dc8229b397df8faadec86bc3d1bf5_l3.png)
![Rendered by QuickLaTeX.com \left [ x<\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-5fe59560429192c0c5955eed241d455b_l3.png)

 Ossia si consideri che:
Ossia si consideri che: [WpProQuiz 16]
[WpProQuiz 16] [WpProQuiz 10]
[WpProQuiz 10] [WpProQuiz 15]
[WpProQuiz 15]