Data la funzione:
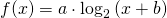
a) calcola a e b sapendo che il suo grafico passa per l’origine e interseca la retta di equazione y=4 nel punto di ascissa 3.
b) rappresenta il grafico di f(x) per i valori di a e b trovati
c) risolvi analiticamente e graficamente la disequazione:
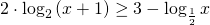
Sviluppo.
a) Passando per l’origine deve essere soddisfatta la
(1) 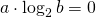
e affermare che interseca una retta in un particolare punto significa che quel punto appartiene alla curva per cui deve valere anche questa relazione:
(2) 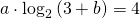
analizzando la (1)
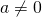
perché se così non fosse la funzione di partenza degenerebbe in un punto coincidente con l’origine.
Risolvo l’equazione:
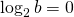
che equivale a scrivere (partendo dalla definizione stessa di logaritmo)
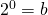
che fornisce il valore
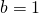 .
.
Sostituendo adesso il valore trovato nella (2) si deve risolvere l’equazione:
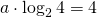
ma
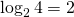 .
.
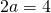 .
.
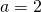 .
.
la funzione di partenza diventa:
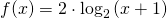
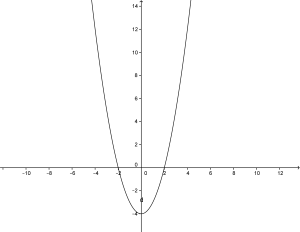
b) Per rappresentare la funzione
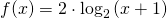
posso non utilizzare le conoscenze della derivata per la sua rappresentazione partendo dal grafico della funzione
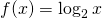
che è:
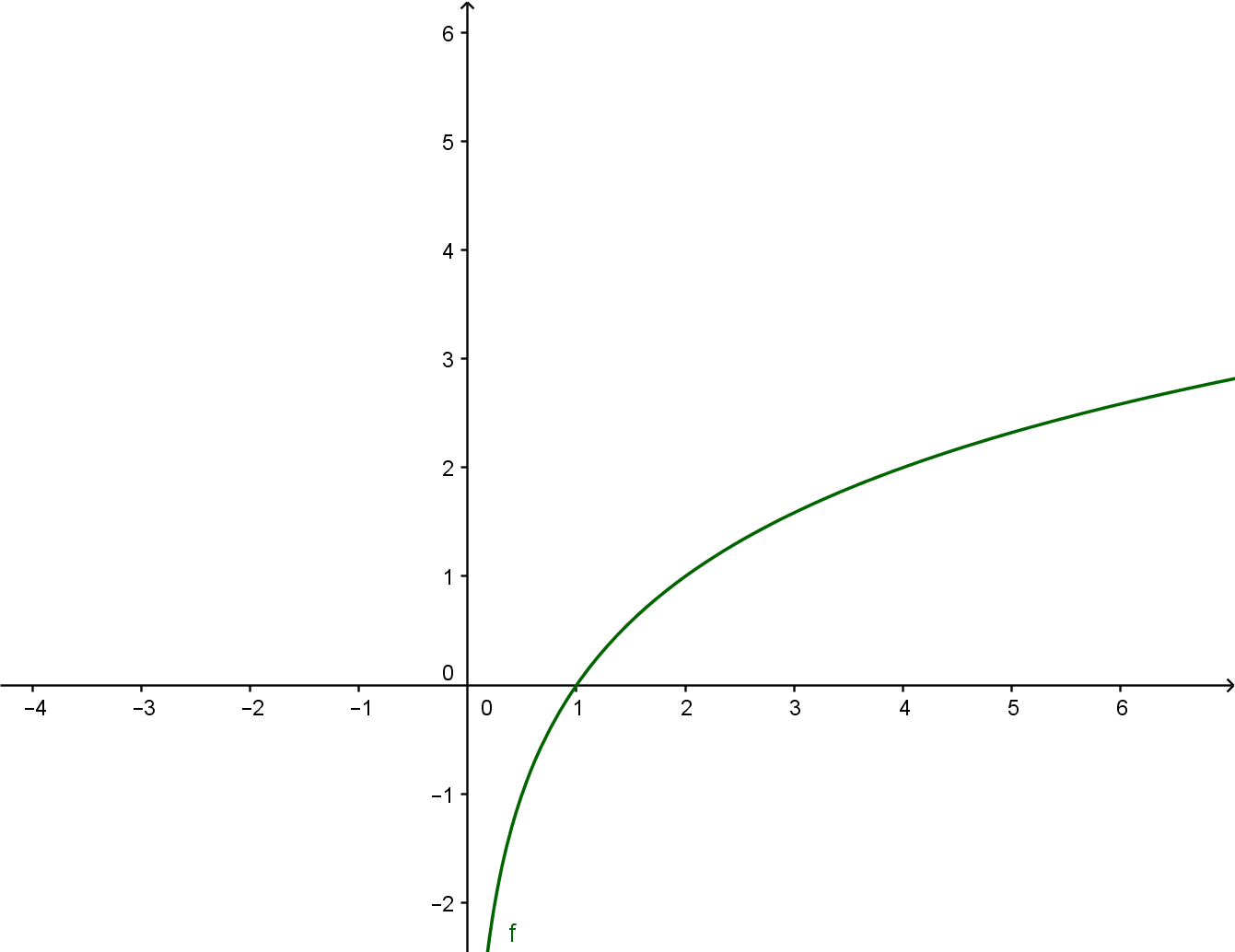 ” width=”1341″ height=”1034″ />
” width=”1341″ height=”1034″ />
La moltiplicazione per 2 fa sì soltanto che sia un po’ più alta (si noti la linea rossa) e che tenda meno velocemente allo 0.
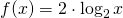
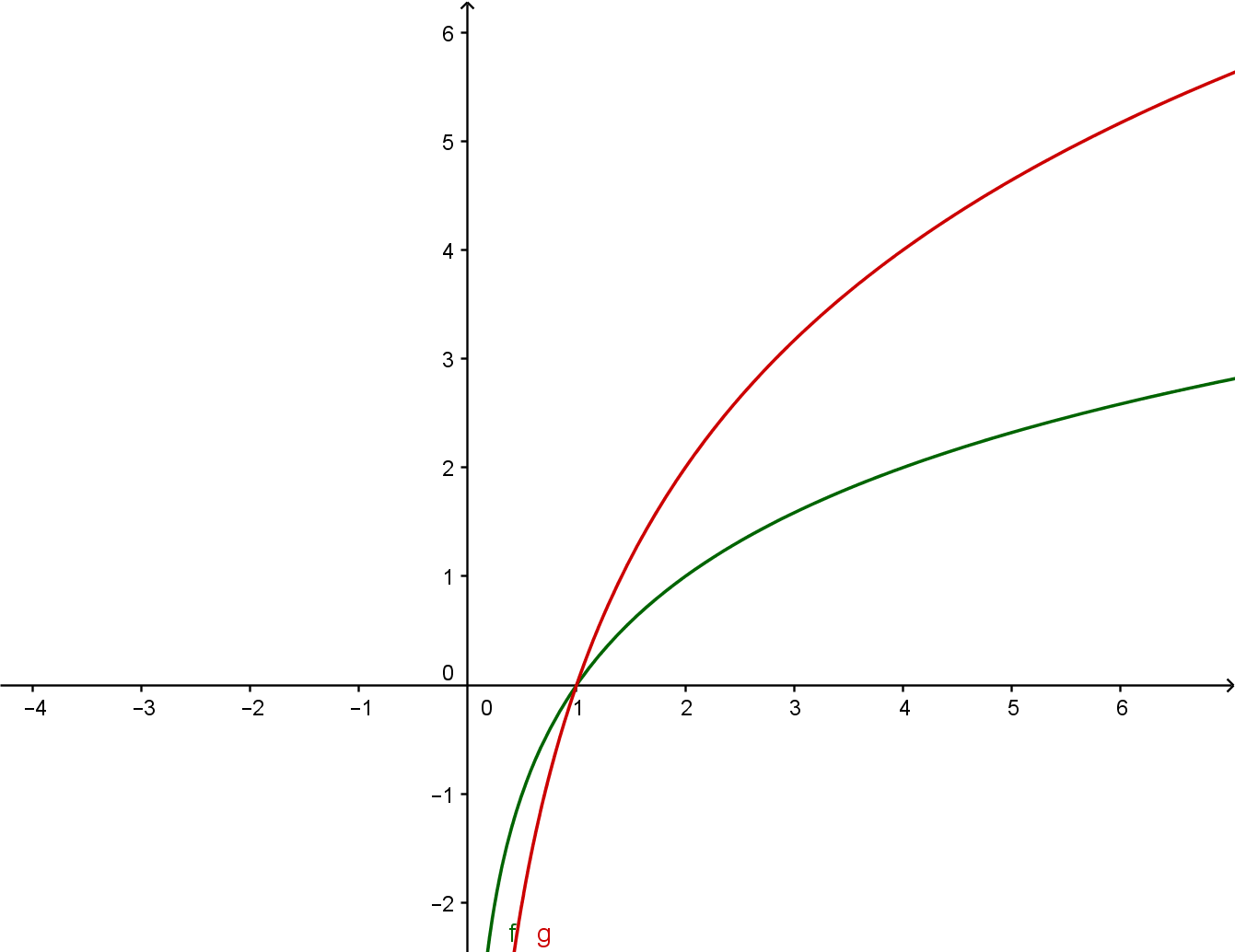
sommare 1 all’argomento della radice significa traslare all’indietro il grafico (linea blu identificata con la lettera h) con asintoto in x=-1
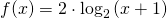
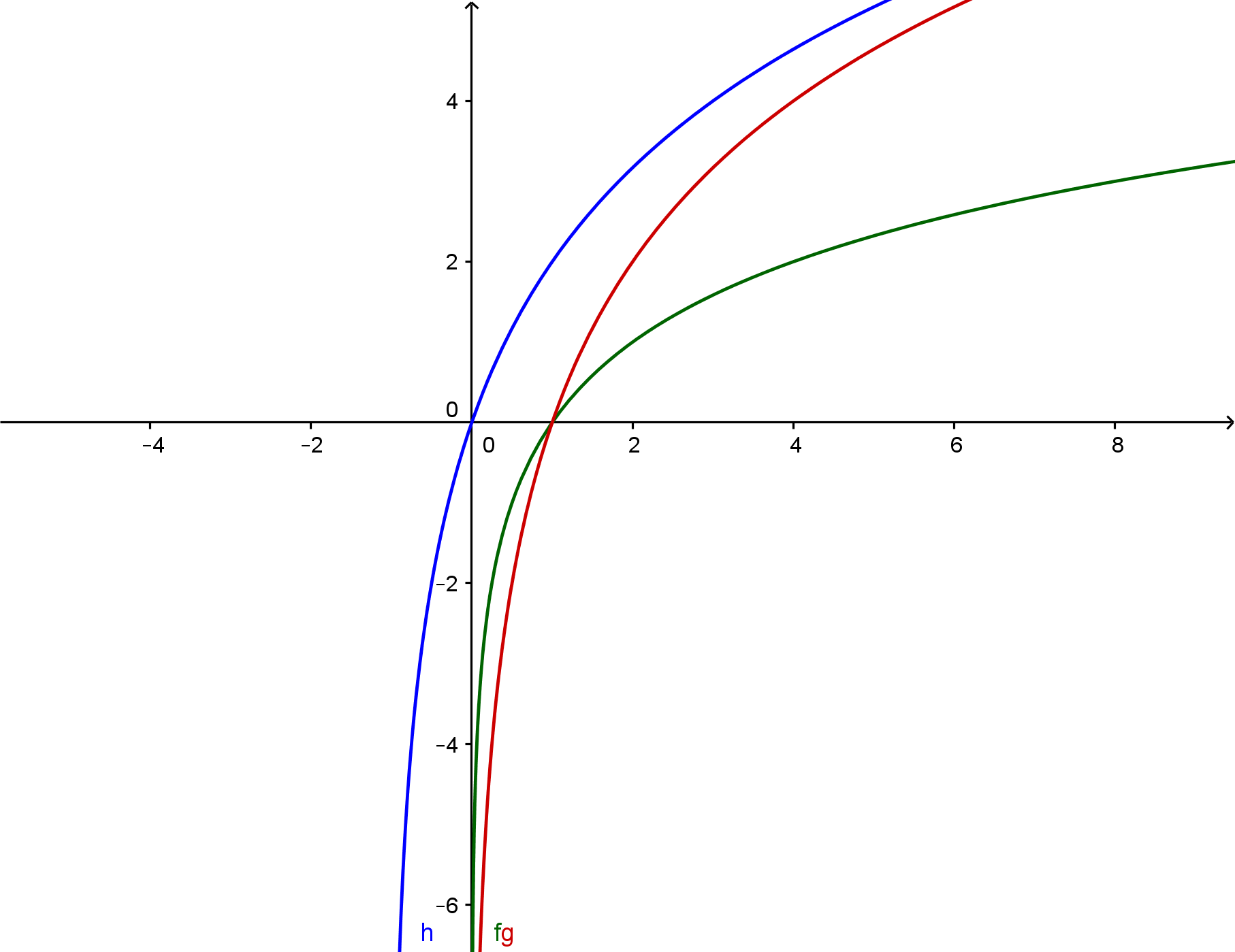
c) Risolvo adesso analiticamente la disequazione:
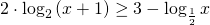 .
.
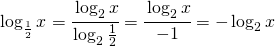
che diventa:
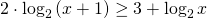 .
.
il dominio è dato dallo studio del sistema di disequazione fornito dagli argomenti dei due logaritmi ossia:
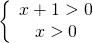
che mi dà come soluzione
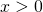
torno alla disequazione che diventa:
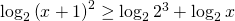 .
.
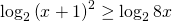
Avendo la stessa base ed essendo questa maggiore di 1 posso studiare la disequazione:
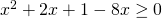 .
.
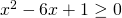
Risolvo l’equazione associata:
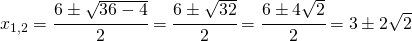 .
.
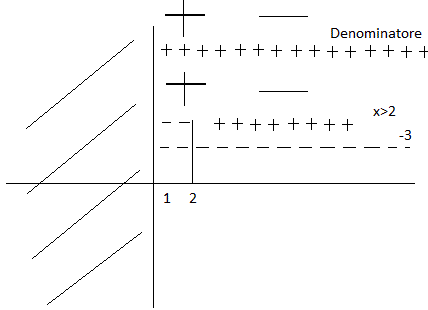
per risolvere la disequazione di secondo grado uso il metodo della parabola ossia:
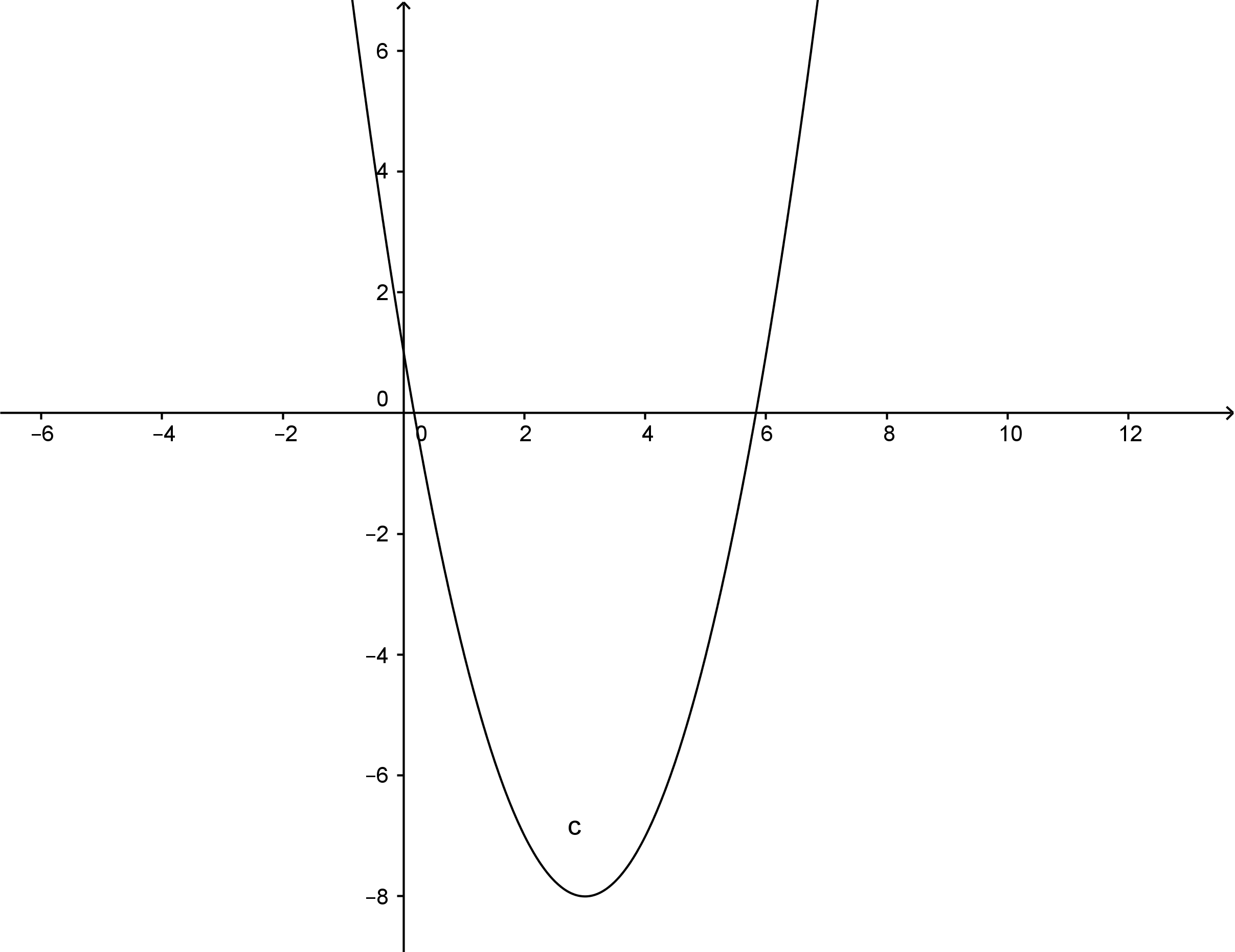 i punti d’intersezione con l’asse x sono le soluzioni precedentemente trovate.
i punti d’intersezione con l’asse x sono le soluzioni precedentemente trovate.
I valori per cui la parabola è maggiore di zero sono i valori esterni ma ricordandomi anche il dominio che era:
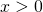
la soluzione della disequazione diventa:
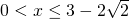
e
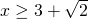 .
.
Per risolverla graficamente studio le seguenti due funzioni:
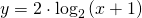
identificata con la linea rossa
e al funzione:
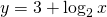
identificata con la linea blu.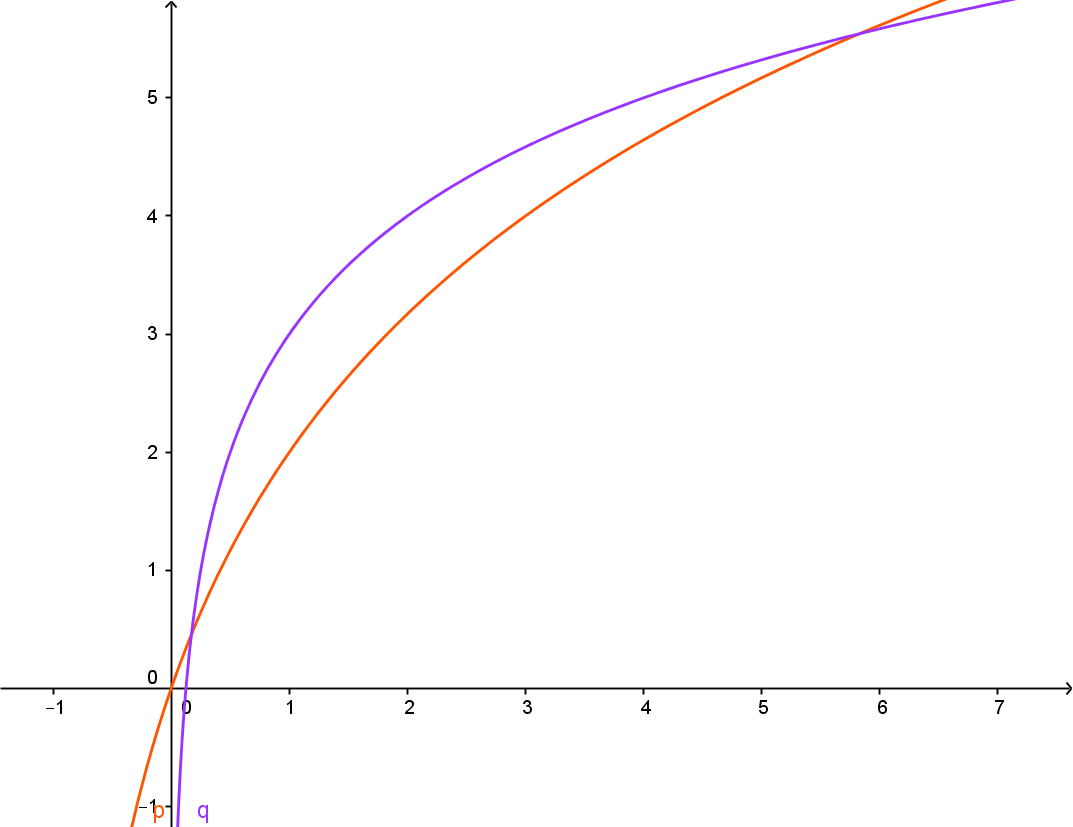 si nota infatti che la linea rossa è sopra a quella blu per i valori precedentemente trovati analiticamente.
si nota infatti che la linea rossa è sopra a quella blu per i valori precedentemente trovati analiticamente.


 Determinare il massimo ed il minimo assoluti della funzione:
Determinare il massimo ed il minimo assoluti della funzione:![Rendered by QuickLaTeX.com \left [ -2;-\cfrac{1}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-f1673929900f5e8c9a8d7064997636d4_l3.png)
 [WpProQuiz 5]
[WpProQuiz 5]

 i punti d’intersezione con l’asse x sono le soluzioni precedentemente trovate.
i punti d’intersezione con l’asse x sono le soluzioni precedentemente trovate. si nota infatti che la linea rossa è sopra a quella blu per i valori precedentemente trovati analiticamente.
si nota infatti che la linea rossa è sopra a quella blu per i valori precedentemente trovati analiticamente.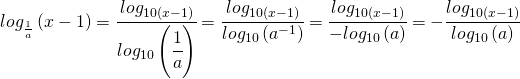
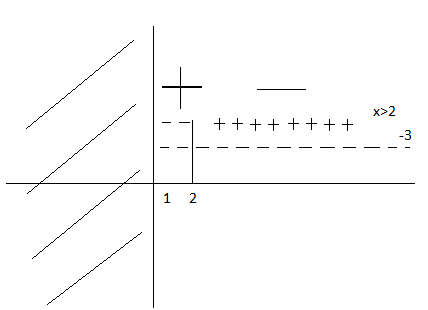
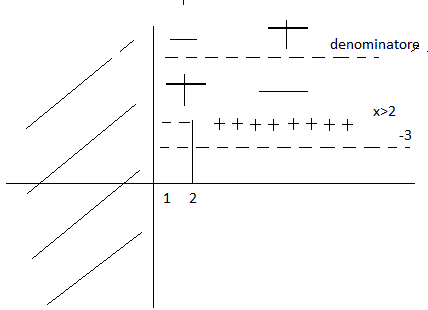

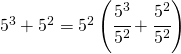

![Rendered by QuickLaTeX.com \left [ \left ( 1,\cfrac{3}{2} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-bc1069d7f684e3b18c1030db0db3c4be_l3.png)
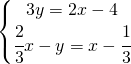
![Rendered by QuickLaTeX.com \left [ \left ( \cfrac{5}{3},-\cfrac{2}{9} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-97bb486ade1c64964c37a04a3fde6c30_l3.png)
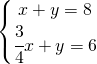
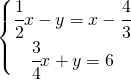
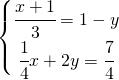
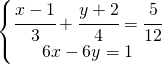
![Rendered by QuickLaTeX.com \left [ \left (\cfrac{1}{2},\cfrac{1}{3} \right ) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-801c5aa12d2b23cdf869d61901284917_l3.png)
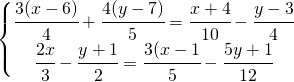
 [WpProQuiz 2]
[WpProQuiz 2]