SCIENZE E TECNOLOGIE INFORMATICHE

Quando si affronta il luogo dei punti del piano di nome parabola ci si imbatte inevitabilmente nel cercare di risolvere le equazioni di secondo grado.

Un’equazione di secondo grado si presenta nella forma:

Per risolverla si deve applicare la seguente formula risolutiva:

Si devono notare alcune cose:

La prima:

significa che si hanno 2 soluzioni che per distinguerle si indica appunto

e

La seconda:

è una radice quadrata e come tale deve avere al suo interno (argomento) il segno positivo.

Quest’affermazione di declina verificando che l’operazione

debba dare sempre una quantità positiva o nulla.

Nel caso in cui si abbia una quantità positiva significa che ho 2 soluzioni

Nel caso in cui ho una quantità pari a zero ho una sola soluzione

Nel caso in cui ho una quantità negativa non ho soluzioni .

Affrontando in classe la risoluzione dell’equazione di secondo grado, mi sono accorto che l’applicazione formale della formula risolutiva, sia che si tratti di un’equazione di primo grado o di grado superiore, crea un blocco e l’esclusione immediata di alcuni ragazzi.

Allora ho pensato di illustrare le seguenti situazioni:

1. attraverso un confine una sola volta è un’equazione di primo grado dove il confine o torrente è identificato dall’asse x

2. attraverso il confine due volte: ho un’equazione di secondo grado:

3. attraverso il confine tre volte: ho un’equazione di terzo grado:

Potrei avere magari comunque un’equazione di secondo grado ma essa tocca solo una volta il mare! Guardando la figura esplico il mio pensiero:

Come si vede la linea immaginaria tra la montagna ed il cielo forma una parabola e sembra che il cielo tocchi il mare solo in un punto.

Date le seguenti rette rappresentarle sul piano e determinare il loro punto di intersezione se esiste:

1) tra e

2) tra e

Data la retta:

e la retta:

trovare l’eventuale punto d’intersezione sia rappresentandole entrambe sullo stesso piano cartesiano che attraverso la risoluzione del sistema d’equazione di primo grado applicando il metodo risolutivo che si preferisce.

Per questo post ringrazio un ragazzo del liceo scientifico che mi ha stimolato a scriverlo.

Data la funzione trigonometrica:

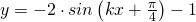
determinarne il codominio e la periodicità ed il valore di 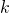 affinché abbia periodicità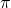

Per arrivare alla soluzione vi sono diverse strade ma la più stimolante è sicuramente utilizzare le trasformazioni.

So che la funzione:

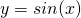
ha periodicità 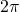e codominio tra [-1 e 1].

Per inciso il codominio di una funzione è l’intervallo aperto o chiuso entro il quale la y assume determinati valori.

Infatti il grafico è:

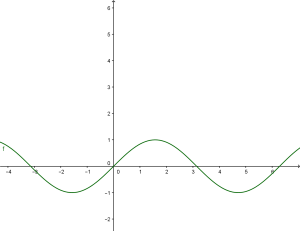
y=sin(x)

Parto da quest’ultima per arrivare a quella di partenza.

Parto da questa:

(1)

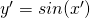
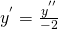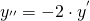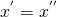pongo e quindi e  quindi la (1) diventa:

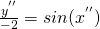ossia:

(2)

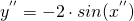
In questo caso il codominio qual è?

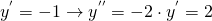
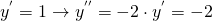
il codominio è tra [-2;2]. Lo si vede anche dal seguente grafico:

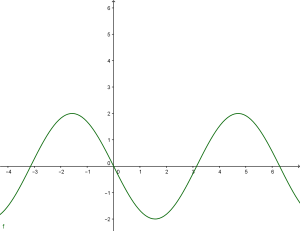
y”=-2sin(x”)

adesso applico la seguente trasformazione:

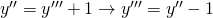lasciando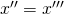

che permette di avere la (2) trasformata in:

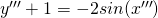
che diventa

(3)

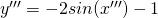
il codominio prima era tra [-2;2] quindi diventa:

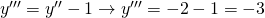
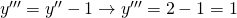
ossia il codominio è tra [-3;1] che si vede anche dal grafico:

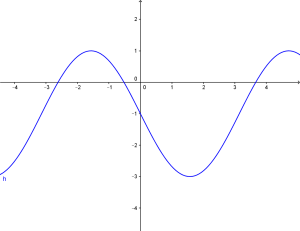
y”’=-2sin(x”’)-1

Adesso applico la trasformazione:

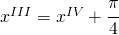e

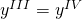
quindi la (3) diventa:

(4)

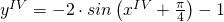
questa trasformazione non cambia la periodicità della mia funzione in quanto sommare o sottrarre una quantità all’argomento del seno fa sì che l’andamento periodico della funzione si sposti in avanti o indietro.

Infatti il grafico della (4) è uguale a quello della (3) solo spostato indietro:

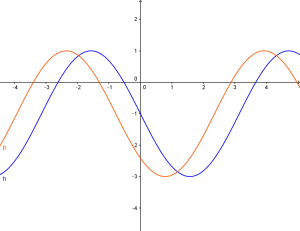
la linea blu identifica la curva (3) mentre quella rossa la curva (4) che è uguale solo spostata all’indietro di .

Ultima trasformazione che va ad influire sul calcolo della periodicità.

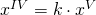e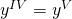

allora la (4) diventa:

(5)

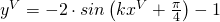
la periodicità diventa:

.

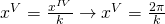ossia è .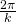

Se io volessi trovare il valore di k per cui la periodicità sia 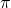è sufficiente quindi risolvere questa semplice equazione:

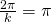
che fornisce come soluzione 2!

Renè Magritte

Provare a risolvere le seguenti equazioni frazionarie in un’ora:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

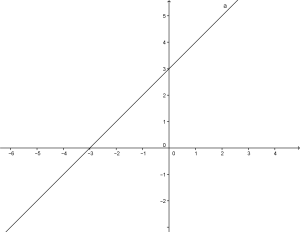
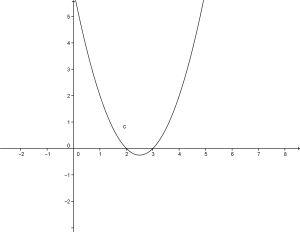
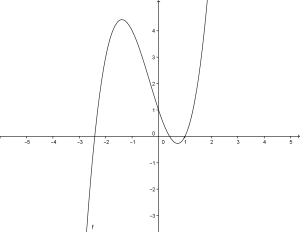
Affermare che un punto appartiene ad una retta implica il fatto che si debba verificare che le coordinate del punto sostituite all’equazione della retta diano un’identità.

Dato un punto

con e , intendo la coordinata x e la coordinata y del mio generico punto P. Ad esempio P potrebbe avere le coordinate 3 e 4 ed indentificarlo quindi come

P(3;4) con  e

perché questo punto appartenga ad r e si indica come

si devono sostituire le sue coordinate x e y nell’equazione della retta:

ossia data una retta:

la relazione

deve essere un’identità.

Ad esempio dato

P(3;4) verificare che appartenga a

si devono sostituire le sue coordinate e verificare che si abbia un’identità:

y è uguale a 4 mentre x è uguale a 3 quindi:

4 = 3 + 1.

Essa è un’identità ossia la parte di sinistra è uguale alla parte di destra.

e si indica appunto che 

ma il punto G(5;15) appartiene alla retta?

Si sviluppa il problema nella stesa maniera:

x=5 mentre y=15 …

15 = 5 +1

ma 15 non è ugual a 6 per cui il punto G non appartiene alla retta e si indica:

Attenzione ai segni dei denominatori negli esercizi 1 – 2- 3

1)
2)
3)

4)

5)

Renè Magritte

Gli esercizi sono suddivisi per livello.

Il trucco per risolverle è quello di analizzare prima il denominatore e poi fare il minimo comune multiplo tra i denominatori.

Se al denominatore compaiono numeri e polinomi o monomi, fare il m.c.m. prima dei numeri e poi quello tra i monomi o i polinomi.

Esercizi per un livello sufficiente (6):

6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.

Per un livello discreto (7)

Renè Magritte, La sera che cade, 1964

Le equazioni razionali frazionarie sono quelle che non hanno l’incognita sotto radice ma hanno l’incognita al denominatore ed al numeratore.

In pratica un’equazione frazionaria (da adeso in poi continuerò a chiamarla cosi)  è del tipo:

(1)  

Si risolve con i normali metodi di un’equazione di primo grado con un’avvertenza: quando si semplifica il denominatore bisogna studiare il dominio entro il quale l’equazione ha soluzione o più banalmente il CAMPO D’ACCETTABILITA’, meglio ancora, i valori consentiti che risolvono l’equazione.

Per arrivare a risolvere l’equazione usata come esempio, preferisco richiamare come si sviluppa un’espressione con soli numeri, con numeri e lettere per poi arrivare a risolvere la (1).

Prendo l’espressione:

essa si sviluppa prendendo il minimo comune multiplo del denominatore ossia

quindi l’espressione diventa:

Adesso prendo l’espressione:

essa si sviluppa prendendo il minimo comune multiplo del denominatore ossia

quindi l’espressione diventa:

Focalizzo l’attenzione sul denominatore ossia perché possa aver senso, A e B dovranno essere sempre diversi da zero altrimenti dividerei qualcosa per zero e ciò è impossibile.

Adesso torno all’equazione di partenza:

(1)  

Faccio il minimo comune multiplo pensando che

A= x-1

e

B=x-2

Quindi l’equazione diventa:

Studiando il C.A. (campo d’accettabilità) devo porre:

e

Fatto questo posso semplificare il denominatore e risolvo una semplice equazione di primo grado:

che ha come soluzione

Video su un’equazione frazionaria:

Equazione frazionaria