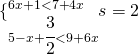Dalla base 5 si è passati alla base 20 che è in realtà un passaggio da quella 10. Si è cominciato perciò a contare usando anche le dita dei piedi. La base 20 è stata usata dai Maya, da alcune tribù africane e sudamericane.
Il sistema a base 20 cominciò a sentire momenti di crisi quando si è cominciato a coprire le dita dei piedi con le scarpe! A questo punto si è cominciato a contare a base 10.
Una base importantissima è la base 12, è stata usata dai Babilonesi, dai Sumeri. La giornata era divisa in 12 periodi di due ore ciascuna, il percorso che impiega il Sole per tornare alla stessa posizione è diviso in 12, lo zodiaco pure. Per i Romani l’unità di misura del peso e moneta è diviso in 12. Per i britanni 1 piede equivale a 12 pollici, 1 pollice a 12 linee, 1 linea a 12 punti.
Da dove nasce l’uso della base 12? Nasce dal contare il numero delle falangi di una mano usando il pollice come cursore, inoltre ha un altro vantaggio ossia quello di avere un numero di divisori superiore a quello della base 10. I divisori del 12 sono 1,2,3,4,6 e 12 mentre la base 10 ha solo 1,2,5,10 e conseguentemente è più facile fare le divisioni in base 12.
La base 12 è usata in India, Indocina, Pakistan, Afghanistan, Iran, Iraq, Turchia, Siria, ed Egitto. Dal punto di vista strettamente linguistico si pensi all’inglese che solo dal numero 13 in poi si usa il suffisso “teen”.
Un’altra base è la base 60 usata dalla civiltà mesopotamiche e dagli astronomi greci. Viene attualmente usata per le misure angolari (latitudine, longitudine), per le misure cronometriche. Si crea la base 60 contando le falangi di una mano ed utilizzando l’altra con le 5 dita per arrivare fino a 60.
Ma perché vince la base 10? Si pensa in seguito alle popolazioni indoeuropee vero il 2500-3000 a.c. La base 10 non ha bisogno di tanti simboli come ad esempio la base 60. Si pensa inoltre che la base 10 permetta un calcolo mnemonico più facile rispetto ad una base 60.
La base 10 permette una tavola delle moltiplicazioni molto semplice, il numero di cifre per rappresentare i numeri è inferiore per basi più piccole.
Ma perché allora non scegliere la base 11 o la base 12? La base 12 ha i seguenti pregi:
- ha più divisori
- l’anno ha un numero di mesi pari a quello dei divisori
- un giorno ha il numero di ore doppie rispetto alla base
- un’ora ed un minuto hanno un numero di minuti e secondi quintupli della base
Un aspetto non di poca rilevanza è che la lingua parlata è stata la prima usata per comunicare e memorizzare i numeri in base 10 è molto più semplice che in altre basi.
La parola fine vien poi data dalla Convenzione di Parigi dopo la Rivoluzione Francese che fissò la numerazione a base 10 come convenzione tra tutti gli Stati Europei.