
Vasilij Kandinski
Spesso si parla di sistema informativo e sistema informatico come se fossero un unicum; è corretto distinguerli.
Per sistema informativo si intende l’insieme di strumenti automatici, procedure manuali, risorse umane e materiali, norme organizzative, orientato alla gestione delle informazioni.
Per sistema informatico (EDP = Electronic Data Processing) è un sottoinsieme del sistema informativo che si dedica solo alla gestione automatica delle informazioni.
Il sistema informativo è composto da: archivi e applicazioni che formano il software, e supporti fisici e strumentazione che formano i componenti dell’hardware.
Per rafforzare l’importanza dei database si pensi sempre alla gestione del magazzino. Mentre una persona sta aggiornando le scorte, nel negozio si continua a vendere la merce. Entrambe le persone devono accedere al file che gestisce il magazzino ma non possono accedervi contemporaneamente in quanto per leggere o scrivere un file bisogna dire al sistema che in quel momento ho aperto il file.
Ad esempio si provi a condividere un file di word da un disco di rete. (Si intende uno spazio di memoria condiviso da più PC), il messaggio che compare è ce se si vuole fare una copia del file si può fare ma poi quando si va a salvarlo cosa succede all’altra copia che sta venendo usata dall’altra persona?
Si generano i seguenti problemi:
– incongruenza: il pezzo si troverebbe in quantitativi diversi rispetto al file che tiene questa informazione
– inconsistenza: il dato non ha più significato diventando inutilizzabile
– ripetizione del dato: il dato viene ripetuto in moltissimi file che utilizzano quel quantitativo
Un database per essere definito in maniera corretta dovrebbe rispettare sempre i seguenti vincoli:
1 – indipendenza dalla struttura fisica dei dati: ossia cambiare i supporti di memoria su cui vengono scritti i dati non devono inficiare la struttura
2- indipendenza logica: se devo aggiungere una caratteristica al pezzo di magazzino ad esempio le sue dimensioni, il programma che estrae il quantitativo deve continuare a funzionare anche se è stato aggiunta una nuova descrizione
DBMS
Database Management System
Il programma che evita i dati ripetuti, l’incongruenza, l’inconsistenza è il DBMS.
Il suo compito è:
gestione di grandi moli di dati: si evitano i dati ridondanti ossia le ripetizioni
condivisione: lo stesso dato viene condiviso da molti utenti senza che per questo rimangano dati non veritieri; ad esempio nel caso dell’aggiornamento del magazzino e della vendita del pezzo, il DBMS riesce a mantenere sempre il quantitativo corretto del pezzo con opportuni meccanismi di gestione delle collisioni.
persistenza: controllo agli accessi dei dati mediante opportune regole di sicurezza, ad esempio non si vuole che il commesso possa cambiare il prezzo della merce ma solo il responsabile del reparto, entrambi possono accedere al dato ma solo uno dei due può modificarlo.
Maggiori DBMS attualmente in commercio:
– Oracle
–MS SQL server
– MS Access
– Sybase
– Informix
– Ingres
– MySQL
– PostgreSQL
Che differenza intercorre tra Database e DBMS?
In letteratura non si fa distinzione ma in fase didattica per Database intendo la struttura dei dati opportunamente organizzata, mentre per DBMS intendo quel software che garantisce la grande quantità dei dati, la condivisione e la persistenza dei dati.




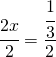


![Rendered by QuickLaTeX.com \left [ x=-\cfrac{2}{3} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9fa13af609c813104501c999fc0ec0e9_l3.png)
![Rendered by QuickLaTeX.com \left [ x=\cfrac{9}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-7bd46b58e1adf1471ebe9113e7594ea5_l3.png)
![Rendered by QuickLaTeX.com \left [ x=\cfrac{3}{2} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4551709c8447bf95863787dc5f06fb05_l3.png)


