Gino Severini
Per risolvere il problema bisogna legger bene le premesse; dipanate opportunamente, lo sviluppo va molto più velocemente di quanto ci si potesse aspettare. E’ solo involuto il testo che presuppone un’immediata intuizione delle funzioni che entrano in gioco.
“Nel primo quadrante del sistema di riferimento Oxy sono assegnati l’arco di circonferenza di
centro O e estremi A(3, 0) e B(0, 3)” è un arco di circonferenza con equazione:
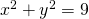 ossia circonfernza con centro in O(0;0) e raggio r=3.
ossia circonfernza con centro in O(0;0) e raggio r=3.
“l’arco L della parabola d’equazione 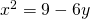 i cui estremi sono il punto A e il punto (0, 3/2).” è una semplicissima parabola con equazione:
i cui estremi sono il punto A e il punto (0, 3/2).” è una semplicissima parabola con equazione:
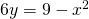 che messo nella forma più conosciuta è:
che messo nella forma più conosciuta è:
(1) 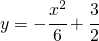
Tale parabola ha concavità verso il basso. Per determinare il vertice calcolo la derivata prima e poi la annullo:
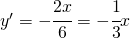 ossia si annulla in
ossia si annulla in 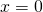 che sostituita nella (1) si trova l’ordinata del vertice che risulta:
che sostituita nella (1) si trova l’ordinata del vertice che risulta:
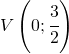
I punti di intersezione sono uno il vertice (con l’asse delle ordinate) ,gli altri si determinano con la condizione 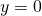 ; i due valori per cui la parabola tocca l’asse delle ascisse sono quelli che risolvono l’equazione di secondo grado:
; i due valori per cui la parabola tocca l’asse delle ascisse sono quelli che risolvono l’equazione di secondo grado:
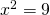 che sono appunto
che sono appunto 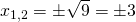 .
.
Adesso si mette il tutto sul piano cartesiano:
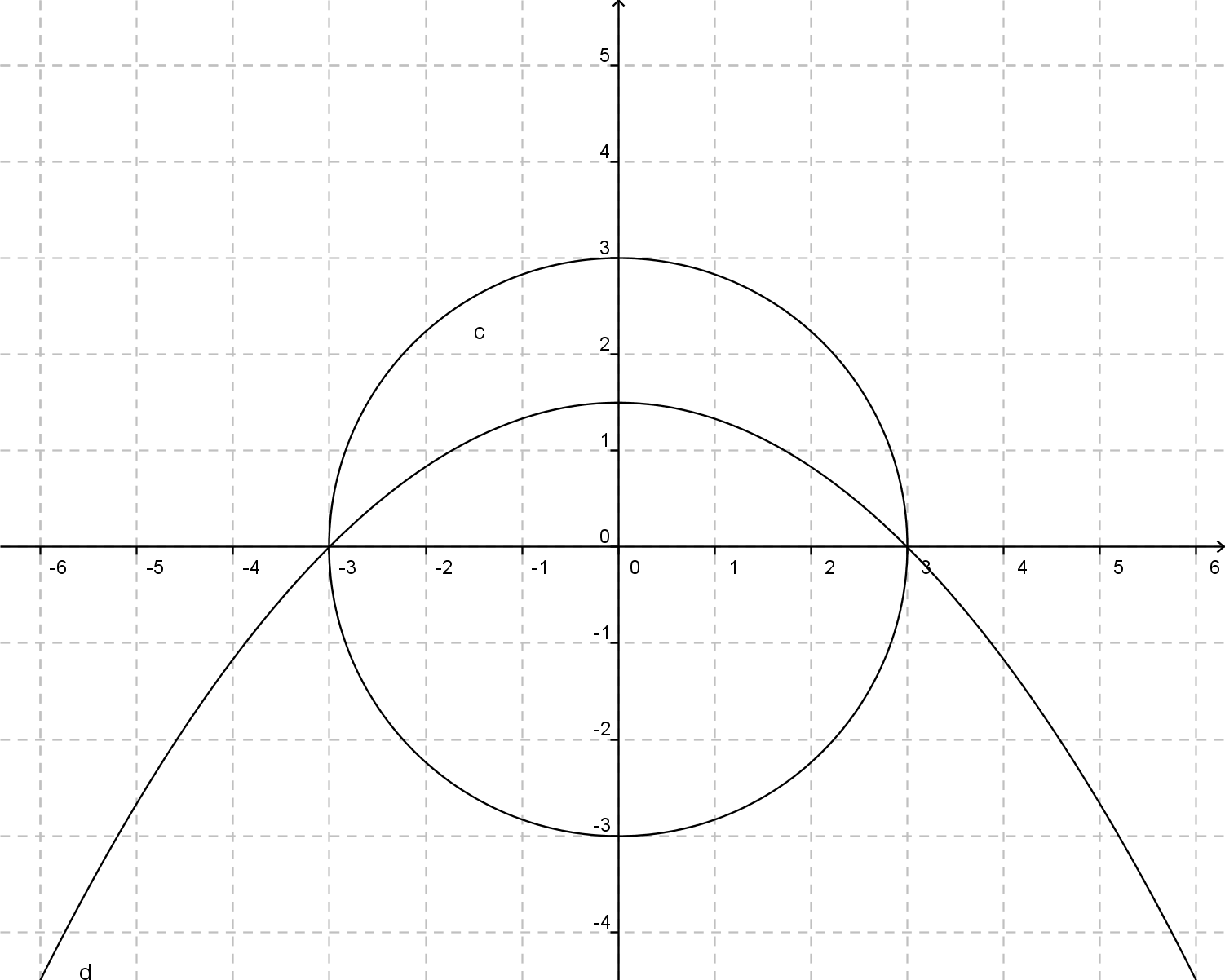
1) Per determinare la retta tangente in A che è un punto di appartenenza della parabola è sufficiente considerare il valore della derivata prima in A.
Retta passante per A ha equazione:
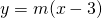 la derivata prima della parabola in A vale
la derivata prima della parabola in A vale 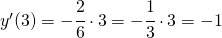
per cui la retta r ha equazione
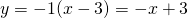
Aggiorno il disegno che permette di capire bene la domanda:
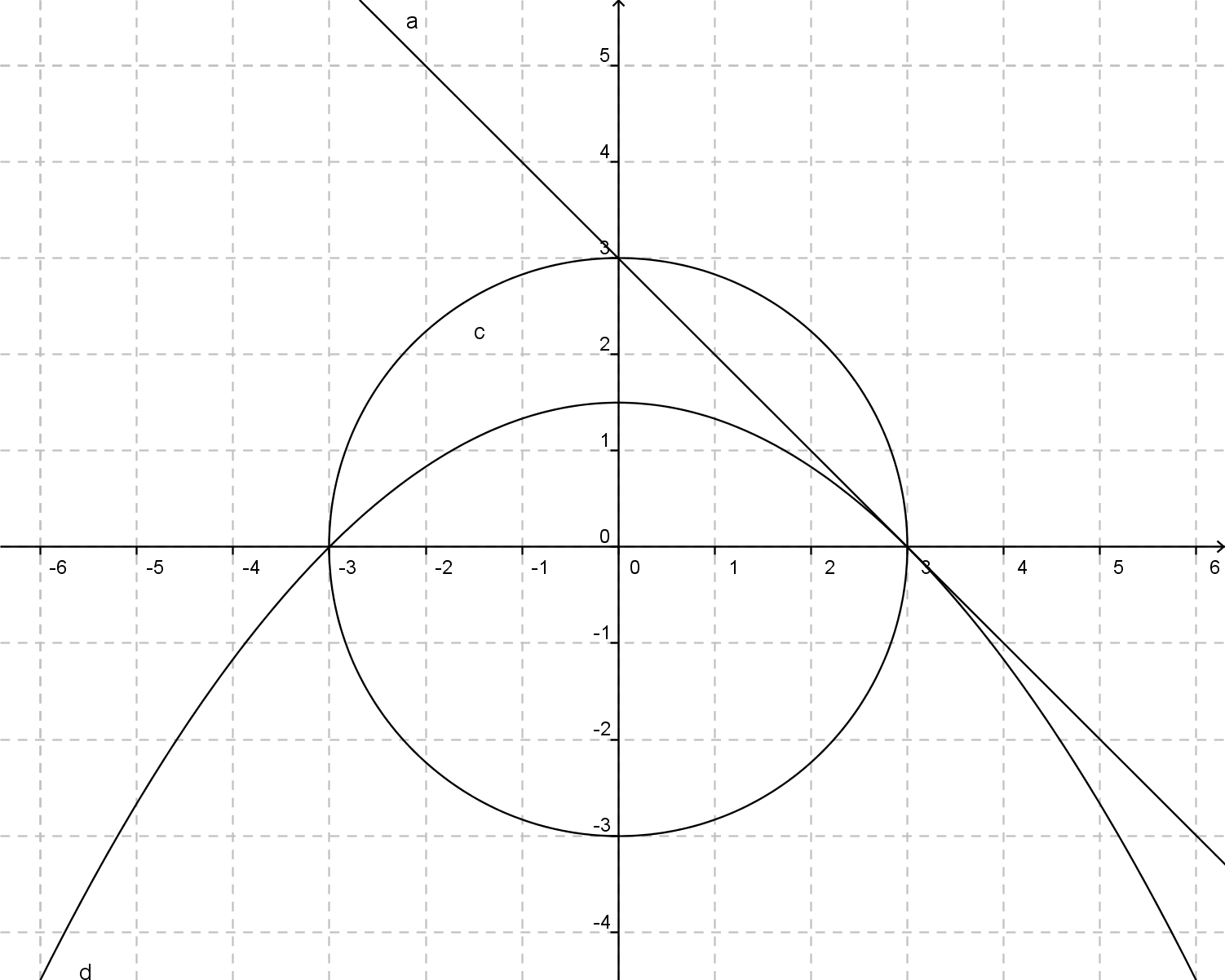 Per calcolare l’area si ha un semplice integrale. Per la parte superiore si fa un quarto di circonferenza di raggio 3 meno il triangolo che forma la retta con gli assi cartesiani, triangolo di base 3 ed altezza 3.
Per calcolare l’area si ha un semplice integrale. Per la parte superiore si fa un quarto di circonferenza di raggio 3 meno il triangolo che forma la retta con gli assi cartesiani, triangolo di base 3 ed altezza 3.
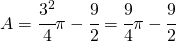 .
.
La parte inferiore invece presuppone sviluppare un integrale:
![Rendered by QuickLaTeX.com \cfrac{9}{2}-\int_{0}^{3}\left(-\cfrac{x^{2}}{6}+\cfrac{3}{2}\right)=\left.\cfrac{9}{2}-\left(-\cfrac{x^{3}}{18}+\cfrac{3}{2}x\right)\right]_{0}^{3}=\cfrac{9}{2}+\cfrac{27}{18}-\cfrac{9}{2}=\cfrac{3}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a3f2836a3aeef0412f531fbf8afc598c_l3.png)
2) La seconda domanda è un’applicazione immediata del concetto di integrale il quale fornisce o un’area se viene data una retta che delimita una parte di piano o un volume se viene data una parte spazio. L’integrale ossia è la sommatoria di tanti infinitesimi. Nel caso specifico si ha l’area di una sezione, sommando tutte le sezioni nell’intervallo dato si ha il volume per cui è sufficiente calcolare l’integrale definito:
![Rendered by QuickLaTeX.com \int_{0}^{3}\left(e^{5-3x}\right)dx=\left.\left(\cfrac{e^{5-3x}}{-3}\right)\right]_{0}^{3}=\cfrac{e^{-4}}{-3}+\cfrac{e^{5}}{3}=\cfrac{e^{5}-e^{-4}}{3}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-eb929451cfbc6b6672c41846f15bd72e_l3.png)
3) Si utilizzi la formula per il calcolo del volume di un solido ottenuto dalla rotazione della differenza di due funzioni che sono:
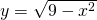 e
e 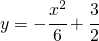 ossia:
ossia:
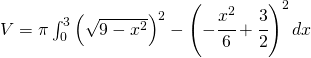 =
=
![Rendered by QuickLaTeX.com \ensuremath{\pi\int_{0}^{3}\left(\cfrac{27}{4}-\cfrac{1}{2}x^{2}-\cfrac{x^{4}}{36}\right)dx=\pi\left.\left(\cfrac{27}{4}x-\cfrac{x^{3}}{6}-\cfrac{x^{5}}{180}\right)\right]_{0}^{3}}=\cfrac{72}{5}\pi](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ffbdaac3a96b9a13ff914d5941305f8f_l3.png)



![Rendered by QuickLaTeX.com 7-\left [ \left ( 3+\cfrac{1}{5}-\cfrac{3}{4}-2 \right )-\left ( \cfrac{2}{5}-6 +\cfrac{3}{4}-\cfrac{1}{2}\right )\right ]+\cfrac{6}{5}-\left ( \cfrac{7}{20}+\cfrac{1}{20} \right )](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-da0b3f7edbbbadcfe17f620fe6f4ebe0_l3.png)
![Rendered by QuickLaTeX.com \cfrac{1}{9}-\cfrac{1}{12}+\left ( \cfrac{1}{8}-\cfrac{23}{9}\right )-\left [ \cfrac{3}{8}+\left ( \cfrac{1}{3}-\cfrac{5}{2} \right )-\cfrac{1}{6} \right ]+\cfrac{4}{9}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a5ecd4db6959f2b853fe2a8e4ca32502_l3.png)
![Rendered by QuickLaTeX.com 4-\left [ 2+\left ( 1-\cfrac{2}{3} \right )-\left ( -4+\cfrac{1}{5} \right ) \right ]+\left [ 7-\left ( 6+\cfrac{1}{15}\right )-\cfrac{2}{5} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-6526835e0af9a125ac20dbc700ffb65a_l3.png)


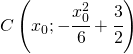 e raggio
e raggio 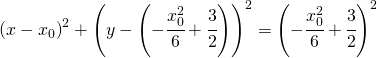

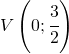


![Rendered by QuickLaTeX.com \cfrac{9}{2}-\int_{0}^{3}\left(-\cfrac{x^{2}}{6}+\cfrac{3}{2}\right)=\left.\cfrac{9}{2}-\left(-\cfrac{x^{3}}{18}+\cfrac{3}{2}x\right)\right]_{0}^{3}=\cfrac{9}{2}+\cfrac{27}{18}-\cfrac{9}{2}=\cfrac{3}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a3f2836a3aeef0412f531fbf8afc598c_l3.png)
![Rendered by QuickLaTeX.com \int_{0}^{3}\left(e^{5-3x}\right)dx=\left.\left(\cfrac{e^{5-3x}}{-3}\right)\right]_{0}^{3}=\cfrac{e^{-4}}{-3}+\cfrac{e^{5}}{3}=\cfrac{e^{5}-e^{-4}}{3}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-eb929451cfbc6b6672c41846f15bd72e_l3.png)
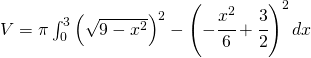 =
=![Rendered by QuickLaTeX.com \ensuremath{\pi\int_{0}^{3}\left(\cfrac{27}{4}-\cfrac{1}{2}x^{2}-\cfrac{x^{4}}{36}\right)dx=\pi\left.\left(\cfrac{27}{4}x-\cfrac{x^{3}}{6}-\cfrac{x^{5}}{180}\right)\right]_{0}^{3}}=\cfrac{72}{5}\pi](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ffbdaac3a96b9a13ff914d5941305f8f_l3.png)