Studio di funzione es – 2 –

Pubblicato il 4 Giugno 2012 da admin

2) y=\cfrac{x+4}{x^{2}}

Ecco il grafico:

Due asintoti: uno verticale ed uno orizzontale

Si noti dove la funzione interseca l’asse delle x e come vi è anche un punto di flesso.

Nessun massimo o minimo

Pubblicato in Uncategorized | Lascia un commento

Studio di funzione es. – 1 –

Pubblicato il 4 Giugno 2012 da admin

1) y=\cfrac{3+x}{x-2}

Ecco il grafico:

Abbiamo due asintoti: uno orizzontale ed uno verticale

Nessun punto di massimo o di minimo.

 

 

Pubblicato in Uncategorized | Lascia un commento

Definizione di funzione – dominio e codominio

Pubblicato il 2 Giugno 2012 da admin

George Seurat

Dato un insieme X ed un insieme Y la relazione tra un elemento di  X  ed un solo elemento di Y si chiama funzione.

Essa si indica con

y=f(x)

L’insieme dei valori di X prende il nome di Dominio mentre i valori di Y prende il nome di codominio.

Esempi di funzione.

1- Per fare una frittata è indispensabile avere il fuoco, una padella, del sale, delle uova, allora potrò dire che

frittata=f(fuoco, padella, sale,uova) ossia è funzione del fuoco, della padella, del sale, delle uova ossia di quattro variabili.

Ad esempio il dominio del fuoco è la presenza dell’ossigeno e del carbonio, senza di questi due elementi il fuoco non esiste.

Studiare funzioni a più dimensioni è complesso e vengono rappresentate da grafici di questo tipo:

ossia della  funzione:

z=sin(x)+cos(y)

Ma per molti fenomeni è sufficiente usare un grafico a due dimensioni ossia studiare funzioni del tipo:

y=f(x)=sin(x)

che hanno un grafico che rappresenta ad esempio il moto armonico ossia l’oscillazione di un pendolo, oppure l’andamento delle maree oppure la tensione elettrica ai capi di una resistenza in regime di corrente alternata.

Pubblicato in Senza categoria | Lascia un commento

Continuità di funzione

Pubblicato il 26 Maggio 2012 da admin
Carlo Carrà

Carlo Carrà

 

Una funzione si dice continua se è possibile disegnarne il grafico senza staccare la matita dal foglio di carta.

Non staccare mai la matita dalla carta equivale a dire che a ogni minimo incremento nella direzione dell’asse x deve corrispondere un altrettanto minimo incremento nella direzione dell’asse y.

Una funzione si dice continua a destra in un punto se incrementando x di un infinitesimo dx, anche la y varia al massimo di un infinitesimo dy.

Una funzione si dice continua a sinistra in un punto se incrementando x di un infinitesimo dx, anche la y varia al massimo di un infinitesimo dy.

Ecco un esempio di funzione continua:

 

 

Pubblicato in Senza categoria | Lascia un commento

Esempi di studio di funzione

Pubblicato il 25 Maggio 2012 da admin

1) y=\cfrac{3+x}{x-2} soluzione

2) y=\cfrac{x+4}{x^{2}} soluzione

3) y=\cfrac{x^{3}+8}{x} soluzione

4) y=\cfrac{4}{x^{2}+3} soluzione

5) y=\cfrac{(x+1)^{3}}{x-1} soluzione

6) y=-\cfrac{(x)^{2}}{8-x^{3}} soluzione

7) y=\cfrac{4x}{2x+1} soluzione

8) y=\cfrac{x^{3}+1}{x^{2}} soluzione

9) y=2x+\cfrac{1}{x-1} soluzione

10) y=\cfrac{x^{2}}{x^{3}-1} soluzione

11) y=\cfrac{x^{2}}{x^{2}+4} soluzione

12) y=\cfrac{x^{2}+2x+1}{2-x} soluzione

13) y=\cfrac{x^{3}-8}{x^{3}} soluzione

14) y=\cfrac{2x}{x^{2}-x-2} soluzione

15) y=\cfrac{4x}{9-x^{2}} soluzione

16) y=\cfrac{2-2x}{4x^{2}+4} soluzione

Pubblicato in Uncategorized | Lascia un commento

Trasformata di Laplace esercizi

Pubblicato il 23 Maggio 2012 da admin

[:it]Trovare l’antitrasformata di Laplace di

a) f(s)=\cfrac{e^{-5s}}{s^{3}}

b) f(s)=\cfrac{e^{-5s}}{(s-2)^{4}}

Sviluppo

a) \cfrac{1}{s^{3}}=L\left [ \cfrac{x^{2}}{2!} \right ]

adesso uniamo il tutto e si ha che:

f(s)=\cfrac{e^{-5s}}{s^{3}}=L\left [\cfrac{(x-5)^{2}}{2!}\cdot H(x-5) \right ]

con H(t-5) è la funzione gradino unitario di Heaviside che è definita così:

H\left ( x-5 \right )=\left{\begin{matrix} 1 & x\geq 5\ 0 & x<5 \end{matrix}\right.

b) Questo secondo esercizio è praticamente uguale al precedente

f(s)=\cfrac{e^{-5s}}{(s-2)^{4}}=L\left [ \cfrac{\left ( t-5 right )^{3}}{6}e^{2(t-5)}cdot H(t-5) \right ]

In particolare notare che l’argomento dell’esponenziale è uguale all’orgomento dell’elevazione al quadrato ed il 2 all’esponente corrisponde al 2 presente al denominatore della trasformata.[:en]

Renè Magritte

Trovare l’antitrasformata di Laplace di

a) f(s)=cfrac{e^{-5s}}{s^{3}}

b) f(s)=cfrac{e^{-5s}}{(s-2)^{4}}

Sviluppo

a) cfrac{1}{s^{3}}=Lleft [ cfrac{x^{2}}{2!} right ]

adesso uniamo il tutto e si ha che:

f(s)=cfrac{e^{-5s}}{s^{3}}=Lleft [ cfrac{(x-5)^{2}}{2!}cdot H(x-5) right ]

con H(t-5) è la funzione gradino unitario di Heaviside che è definita così:

Hleft ( x-5 right )=left{begin{matrix} 1 & xgeq 5\ 0 & x<5 end{matrix}right.

b) Questo secondo esercizio è praticamente uguale al precedente

f(s)=cfrac{e^{-5s}}{(s-2)^{4}}=Lleft [ cfrac{left ( t-5 right )^{3}}{6}e^{2(t-5)}cdot H(t-5) right ]

In particolare notare che l’argomento dell’esponenziale è uguale all’orgomento dell’elevazione al quadrato ed il 2 all’esponente corrisponde al 2 presente al denominatore della trasformata.[:de]

Renè Magritte

Trovare l’antitrasformata di Laplace di

a) f(s)=cfrac{e^{-5s}}{s^{3}}

b) f(s)=cfrac{e^{-5s}}{(s-2)^{4}}

Sviluppo

a) cfrac{1}{s^{3}}=Lleft [ cfrac{x^{2}}{2!} right ]

adesso uniamo il tutto e si ha che:

f(s)=cfrac{e^{-5s}}{s^{3}}=Lleft [ cfrac{(x-5)^{2}}{2!}cdot H(x-5) right ]

con H(t-5) è la funzione gradino unitario di Heaviside che è definita così:

Hleft ( x-5 right )=left{begin{matrix} 1 & xgeq 5\ 0 & x<5 end{matrix}right.

b) Questo secondo esercizio è praticamente uguale al precedente

f(s)=cfrac{e^{-5s}}{(s-2)^{4}}=Lleft [ cfrac{left ( t-5 right )^{3}}{6}e^{2(t-5)}cdot H(t-5) right ]

In particolare notare che l’argomento dell’esponenziale è uguale all’orgomento dell’elevazione al quadrato ed il 2 all’esponente corrisponde al 2 presente al denominatore della trasformata.[:]

Pubblicato in Uncategorized | Lascia un commento

Espressioni frazionarie polinomiali

Pubblicato il 22 Maggio 2012 da admin

Janek Jerka

Le espressioni polinomiali frazionarie sono il primo passo verso le equazioni frazioniarie.

Si sviluppano trovando il minimo comune multiplo del denominatore per poi seguire gli stessi identici passi usati per risolvere le operazioni tra frazioni.

Ecco il primo semplice esempio:

(1) cfrac{1}{x+1}+cfrac{1}{x-1}

Come si risolve?

il m.c.m tra (x+1) e (x-1) è il prodotto tra i due binomi ossia (x+1)cdot (x-1)

quindi la (1) come si risolve?

cfrac{1}{x+1}+cfrac{1}{x-1}=cfrac{(x-1)+(x+1)}{(x+1)(x-1)}=cfrac{2x}{x^{2}-1}

Pubblicato in Uncategorized | Lascia un commento

Dilatazione termica ed esercizi riepilogativi.

Pubblicato il 17 Maggio 2012 da admin

DILATAZIONE TERMICA

● Un ponte in ferro [λ = 1,2 • 10 -5(°C) -1] alla temperatura di 35 °C ha una lunghezza di 45 m. Trovare la sua lunghezza quando la temperatura è di 0°C.

● Un ponte in ferro,[λ = 1,2 • 10 -5(°C) -1] , ha una lunghezza di 45 m. Quale sarà la sua lunghezza quando la temperatura passerà da 0°C a 35 °C ?

ESERCIZI RIEPILOGATIVI SU PESO SPECIFICO E DENSITÀ.

● Un oggetto d’alluminio di 2 cm3 di volume, pesa 5,4 grammi. Calcola il suo peso specifico.

● Determina il volume di 7 Kg di benzina, sapendo che il peso specifico è di 700 Kg/m3.

● La densità del corpo umano è di circa 980 Kg/m3. Conoscendo il tuo peso ( cioè la tua massa) sei in grado di calcolare il volume che occupi?

Pubblicato in Uncategorized | Lascia un commento

Applicazione immediata m.c.m e M.C.D

Pubblicato il 17 Maggio 2012 da admin

Quando si affrontano le equazioni frazionarie e la semplificazione tra polinomi è inispensabile conoscere rispettivamente il m.c.m e M.C.D.

Ecco il primo esempio:

\cfrac{1}{a^{4}}+\cfrac{1}{a^{10}}+\cfrac{1}{a^{16}}

Come si sviluppa?

Si deve fare il m.c.m del denominatore per svilupparlo ossia:

\cfrac{a^{12}+a^{6}+1}{a^{16}}

se ci si ricorda la somma tra frazioni si è sviluppato lo stesso procedimento!

Sviluppare adesso  i seguenti esercizi:

al denominatore vi sarà sempre il m.cm.!

1)  \cfrac{7}{a}+\cfrac{8}{b}+\cfrac{6}{ab}

2) \cfrac{7}{x}+\cfrac{8}{x^{2}}

3) \cfrac{3a}{5b}+\cfrac{5b}{3a}

4) \cfrac{1}{x^{2}}+\cfrac{1}{3xy}+\cfrac{1}{4a}

5) \cfrac{1}{2x}+\cfrac{1}{4y}+\cfrac{1}{8x}

Applicazioni per il M.C.D.

al numeratore di dovrà fare il M.C.D!

1) \cfrac{3x^{2}+4x}{x}

2) \cfrac{4a^{2}+4a^{6}+3a^{4}}{4ax}

Pubblicato in Uncategorized | Lascia un commento

Le disequazioni: primi esercizi

Pubblicato il 17 Maggio 2012 da admin

Carlo Carrà

Si risolvano le seguenti disequazioni di primo grado:

  1. 3x-1<7
  2. 3(x-7)\geq\cfrac{1}{2}x
  3. 3(x+1)^2 \leq\cfrac{1}{3}(3x-1)^2
  4. 3\left(x-\cfrac{1}{2}\right) < 7(x+1)
  5. \cfrac{x^4-1}{x^2+1} \geq \cfrac{1}{4}(2x+1)^2
  6. (x+1)(x-1) \leq \cfrac{1}{9}(3x+6)^2
  7. \left(3x+6\right)^2 - \left(3x-6\right)^2 \leq 11\left(x+2\right)
  8. \left(4x+2\right)\left(4x-2\right) + \left(4x-2\right)\cdot 3\geq \left(4x-7\right)^2 + \left(6x+5\right)\cdot 3
  9. (x-1)(x-2)(x-3)-1>(x-1)^{3}-3x^{2}
  10. 4 [5-2(1-y) ]+2(y-1)>0
  11. 5{ -1+4x-2 [ x-(2-x)-3]-x+2 }>3(x-1)-x+2

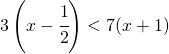
Prerequisiti:

Pubblicato in Senza categoria | Contrassegnato , , , | Lascia un commento