Studio di funzione: protocollo di sviluppo

Pubblicato il 9 Maggio 2012 da admin

Renè Magritte

Per essere in grado di sviluppare lo studio di funzione è molto utile seguire il seguente protocollo che vuole essere una guida in passi per arrivare al grafico finale.

1- Definire il dominio

2- Scrivere il segno della funzione

3- Verifica della presenza di asintoti verticali, orizzontali, obliqui attraverso i relativi limiti.

4- Determinazione dei massimi e minimi attraverso lo studio della derivata prima: annullamento della derivata prima mi fornisce l’ascissa dei punti di massimo o minimo relativi mentre lo studio della disequazione mi indica se effettivamente vi è un massimo o minimo e se è un massimo o minimo.

5- intersezioni con gli assi

CONCLUSIONE Grafico della funzione.

Per fare il grafico si seguano i seguenti passi.

1 – segnare i punti di massimo o minimo

2- segnare i punti di intersezione

3- disegnare con una linea tratteggiata gli eventuali asintoti

4- tracciare il grafico seguendo le indicazioni fornite da tutti i punti precedenti

Pubblicato in Uncategorized | Lascia un commento

Esercizi sui limiti

Pubblicato il 6 Maggio 2012 da admin

Renè Magritte

Possono essere risolti con le metodologie che si ritengono più opportune.Per risolvere un limite comunque si deve cercare di sostituire il valore a cui tende la x all’interno della funzione, dopo si scegli la strada più opportuna.

(1) \underset{x\rightarrow4}{lim}\cfrac{x-4}{2x-8}.

(2) \underset{x\rightarrow\frac{1}{2}}{lim}\cfrac{2x-1}{4x-2}

(3) \underset{x\rightarrow1}{lim}\cfrac{x^{2}-2x+1}{x-1}

(4) \underset{x\rightarrow1}{lim}\cfrac{x-1}{x^{2}-1}

(5) \underset{x\rightarrow2}{lim}\cfrac{x^{2}-2x}{\left(x-2\right)^{2}}

(6) \underset{x\rightarrow-4}{lim}\cfrac{4+x}{16-x^{2}}

(7) \underset{x\rightarrow1}{lim}\cfrac{x^{2}-3x+2}{x^{2}-4x+3}

(8) \underset{x\rightarrow\frac{1}{2}}{lim}\cfrac{\left(2x-1\right)^{2}}{6x-3}

(9) \underset{x\rightarrow1}{lim}\cfrac{2x^{2}-x-1}{2x-2}

(10) \underset{x\rightarrow-\frac{1}{3}}{lim}\cfrac{27x^{3}+1}{3x+1}

(11) \underset{x\rightarrow-\frac{1}{3}}{lim}\cfrac{27x^{3}+1}{3x+1}

(12) \underset{x\rightarrow a}{lim}\cfrac{x^{2}-ax+4x-4a}{3x-3a}

(13) \underset{x\rightarrow-1}{lim}\cfrac{x^{2}+3x+2}{x+1}

(14) \underset{x\rightarrow1}{lim}\cfrac{x-1}{x^{2}-6x+5}

(15) \underset{x\rightarrow3}{lim}\cfrac{x^{2}-6x-9}{x^{2}-2x-3}

Pubblicato in Uncategorized | Lascia un commento

Forma indeterminata: regola di De L’Hospital

Pubblicato il 6 Maggio 2012 da admin
Renè Magritte

Renè Magritte

La regola di De L’Hospital è utilissima nel calcolo dei limiti che si presentano nella forma indeterminata.Si pensi che il marchese De l’Hospital visse nella metà del 1600 ed era allievo di Bernoulli; quest’ultimo fu un grande matematico svizzero esperto di calcolo differenziale e integrale: in tale famiglia sicuramente la matematica e la fisica eranon di casa. Il conosciuto teorema di Bernoulli, applicato nella dinamica dei fluidi e che giustifica il volo degli aerei,  è stato elaborato dal figlio.

Ritengo fondamentale che la trattazione dell’analisi ponga l’argomento delle derivate dopo quello dei limiti e che quest’ultimi vengano spiegati tramite la teoria NSA; grazie a ciò l’applicazione del menzionato teorema ha la sua massima valenza.

Ecco il teorema:

Se sviluppando un limite ci si trova nella forma:

\cfrac{0}{0}

oppure nella forma:

\cfrac{\infty}{\infty}

allora si può applicare il teorema:

(1) \underset{x\rightarrow c}{lim}\cfrac{f(x)}{g(x)}=\underset{x\rightarrow c}{lim}\cfrac{f'(x)}{g'(x)}

ossia posso fare la derivata del numeratore e del denominatore

N.B. NON LA DERIVATA DEL QUOZIENTE DI FUNZIONE ma la DERIVATA DEL NUMERATORE E DEL DENOMINATORE!

La (1) vale anche in questo caso:

(2) \underset{x\rightarrow\infty}{lim}\cfrac{f(x)}{g(x)}=\underset{x\rightarrow\infty}{lim}\cfrac{f'(x)}{g'(x)}

Esempio nel caso \cfrac{0}{0}

\underset{x\rightarrow1}{lim}\cfrac{2x^{2}-2x}{x-1}=\underset{x\rightarrow1}{lim}\cfrac{4x-2}{1}=2

Esempio nel caso \cfrac{\infty}{\infty}

\underset{x\rightarrow\infty}{lim}\cfrac{2x-1}{3x+1}=\underset{x\rightarrow\infty}{lim}\cfrac{2}{3}=\cfrac{2}{3}

Pubblicato in Senza categoria | Contrassegnato , , | Lascia un commento

Limiti: asintoto obliquo

Pubblicato il 6 Maggio 2012 da admin

Renè Magritte

Una retta sul piano può essere parallela all’asse delle ascisse (orizzontale), parallela all’asse delle ordinate (verticale) e quindi, conseguentemente anche obliqua.

In maniera analoga un asintoto può essere verticale, orizzontale ed obliquo.

Per la presenza di un asintoto obliquo DEVONO essere vere le seguenti due condizioni basta che una delle due non sia soddisfatta che l’asintoto non sia presente:

(1) \underset{x\rightarrow\infty}{lim}\cfrac{f(x)}{x}=m

che mi fornisce il coefficiente angolare della “retta” asintoto

(2) \underset{x\rightarrow\infty}{lim}\left[f(x)-mx\right]=q

Ribadisco il fatto che è sufficiente che una delle due non sia vera ossia che mi dia un limite non finito affinché non vi sia il limite obliquo.

Ecco immediatamente un esempio:

sia f(x)=\cfrac{3x^{2}}{2x-1}

allora applico la (1)

\underset{x\rightarrow\infty}{lim}\cfrac{\cfrac{3x^{2}}{2x-1}}{x}=\underset{x\rightarrow\infty}{lim}\cfrac{3x^{2}}{2x-1}\cdot\cfrac{1}{x}=\underset{x\rightarrow\infty}{lim}\cfrac{3x}{2x-1}=\cfrac{3}{2}=m

 

adesso applico la (2) per trovare la q

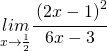
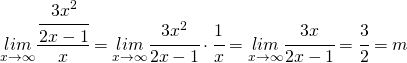
\underset{x\rightarrow\infty}{lim}\left[\cfrac{3x^{2}}{2x-1}-\cfrac{3}{2}x\right]=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-3x(2x-1)}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{6x^{2}-6x^{2}+3x}{(2x-1)\cdot2}=\underset{x\rightarrow\infty}{lim}\cfrac{3x}{4x-2}=\cfrac{3}{4}=q

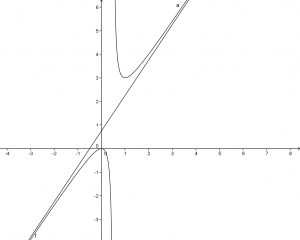
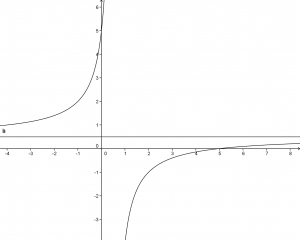
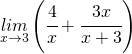l’asintoto è:

y=\cfrac{3}{2}x+\cfrac{3}{4}

Il grafico risulta:

 

Pubblicato in Senza categoria | Lascia un commento

Limiti: asintoto orizzontale

Pubblicato il 6 Maggio 2012 da admin

Renè Magritte

Un asintoto oltre che verticale può essere anche orizzontale, ossia parallelo all’asse delle ascisse.

Per la sua presenza deve valere la seguente relazione:

(1) \underset{x\rightarrow\infty}{lim}f(x)=a

La (1) afferma che quando x assume valori molto grandi, infinitamente grandi, la funzione tende a un valore finito ossia ad un asintoto orizzontale.

Ecco alcuni esempi della presenza di asintoti verticali:

(2) \underset{x\rightarrow+\infty}{lim}\cfrac{x-5}{2x+1}=\cfrac{1}{2}

in questo caso la (2) ci fornisce un asintoto orizzontale con valore

y=\cfrac{1}{2}

Per meglio evidenziare tale fatto ecco il grafico della funzione:

(3) \underset{x\rightarrow-\infty}{lim}\cfrac{4x-5}{2x+6}=2

in questo caso l’asintoto è:

y=2

Ecco il grafico della funzione:

 

 

 

 

 

Pubblicato in Senza categoria | Lascia un commento

Protetto: Materiale per esame ECDL

Pubblicato il 5 Maggio 2012 da admin

Il contenuto è protetto da password. Per visualizzarlo inserisci di seguito la password:

Pubblicato in Uncategorized | Inserisci la tua password per visualizzare i commenti.

Esercizi sul M.C.D. e m.c.m tra monomi

Pubblicato il 3 Maggio 2012 da admin

 

Prima di cominciare gli esercizi, preferisco ridefinire il procedimento.

m.c.m. lettere comuni e non comuni con il massimo esponente.

M.C.D. SOLO lettere comuni con l’esponente più basso

Determinare il m.c.m ed il M.C.D. trai seguenti monomi:

1) a^{4}; a^{10}; a^{16}

2) 5a; 20a; 16a

3) 4a^{4};10a^{4}; 12a^{12}

4) 3a^{3}b^{9};12a^{4}b^{6}; 6a^{6}b^{4}

5) 15a^{3}b; 6a^{2}b^{3}c; 10a^{2}c^{2}

6) -2xy^{3}z; 6x^{3}yz;  8x^{3}z

7) 72a^{3}b^{2}; 18a^{2}b^{3}x^{2}; 15a^{4}b^{4}x

8) \cfrac{1}{4}ab^{2}c^{2}; -3a^{2}b^{2}c^{2}; -\cfrac{1}{2}a^{3}b^{2}c^{2}

Pubblicato in Uncategorized | Lascia un commento

Limiti infiniti: asintoto verticale: approfondimento

Pubblicato il 1 Maggio 2012 da admin

Jacek jerka

Nell’introduzione avevo accennato al fatto che studiare cosa accade ad una funzione nell’intorno di un punto significa studiare il limite a destra e a sinistra.Tale studio, com’è consuetudine, in analisi si riassume in tali forme:

(1) \underset{x\rightarrow c^{+}}{lim}f(x)=\pm\infty

(2) \underset{x\rightarrow c^{-}}{lim}f(x)=\pm\infty

la (1) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore c provenendo da destra.

la (2) descrive il fatto che si studia l’andamento della funzione quando ci si avvicina al valore c provenendo da sinistra.

Ad esempio: assumo che c=2 allora provenire da sinistra significa prendere i seguenti valori: 1,8; 1,9; 1,91 e così via; provenire da destra significa prendere i seguenti valori 2,2; 2,1; 2,001 e così via.

Ancora provenire da destra significa prendere valori >2 mentre provenire da sinistra significa prendere valori <2.

Per capire se la funzione assume un valore +\infty o -\infty si deve studiare il segno della funzione in un intorno del valore a cui tende la x.

Ecco un esempio:

(3) \underset{x\rightarrow2^{+}}{lim}\cfrac{1}{x-2}=+\infty

(4) \underset{x\rightarrow2^{-}}{lim}\cfrac{1}{x-2}=-\infty

Infatti:

– il dominio è tutto Re escludendo il valore in cui si annulla il denominatore ossia 2.

– devo studiare la seguente disequazione:

\cfrac{1}{x-2}>0.

Per x>2 la funzione è positiva mentre per x<2 la funzione è negativa.

La regola è:

per studiare i limiti nella forma (1) e (2) si deve studiare la disequazione della funzione  di cui si deve studiare il limite.

Tale regola giustifica il continuo studio delle disequazioni frazionarie negli anni scolastici precedenti!

Quindi si ha sempre un asintoto verticale ma la funzione ha un andamento diverso.

Il grafico della funzione:

f(x)=\cfrac{1}{x-2} è:

Si nota che:

all’avvicinarsi a 2 da destra la funzione assume valori sempre positivi al limite infinitesimamente positivi;

all’avvicinarsi a 2 da sinistra la funzione assume valori sempre negativi al limite infinitesimamente negativi.

 

Pubblicato in Senza categoria | Lascia un commento

Limiti infiniti – asintoto verticale

Pubblicato il 1 Maggio 2012 da admin

Jacek Yerka

Il concetto di infinito lo si affronta solo all’ultimo anno delle superiori come se esso non fosse già ben presente nella quotidianità.

(1) \underset{x\rightarrow c}{lim}f(x)=+\infty.

(2) \underset{x\rightarrow c}{lim}f(x)=-\infty.

Per dare un’applicazione pratica immediata si sappia che tale limite permette di definire l’asintoto verticale.

Un asintoto è una retta a cui la funzione di partenza tende ad avvicinarsi senza però mai toccarla: asintoto=senza sintesi ossia privo di unione, nel senso che le curve non si toccano.

Si noi che nella (1) e nella (2) ho fatto uso di +\infty e -\infty ossia esiste un infinito positivo ed un infinito negativo: si pensi ai numeri positivi: essi sono infiniti, in senso positivo; mentre quelli negativi sono infiniti in senso negativo.

Per determinare gli asintoti verticali si considerino i punti in cui la funzione non è definita ossia quei punti che sono esclusi dal dominio.

Esempio pratico immediato:

Si consideri la funzione:

f(x)=\cfrac{1}{x^{2}}

essa è definita per ogni valore di x escluso il punto 0.

Studiamo cosa accade un tale punto:

\underset{x\rightarrow0}{lim}\cfrac{1}{x^{2}}=+\infty

ossia se si sostituiscono valori sempre più piccoli di x si noti che il valore della funzione assume sempre valori più grandi: al limite, appunto, ci si trova  con un numero così grande che sinteticamente viene scritto +\infty .

Per completezza e per dare una rappresentazione grafica tale curva, sul piano cartesiano ha il seguente andamento:

Tale curva ha proprio un asintoto verticale coincidente con l’asse delle ordinate.

 

 

Pubblicato in Senza categoria | Lascia un commento

Limiti: esercizi sulla prima definizione

Pubblicato il 1 Maggio 2012 da admin

Jacek Yerka

 

1) \underset{x\rightarrow9}{lim}3-\sqrt{x}.

2) \underset{x\rightarrow2}{lim}\cfrac{x+2}{3x}.

3) \underset{x\rightarrow2}{lim}3^{2-x}.

4) \underset{x\rightarrow1}{lim}\cfrac{x^{2}-3x+2}{x+4}.

5) \underset{x\rightarrow3}{lim}\left(\cfrac{4}{x}+\cfrac{3x}{x+3}\right).

6) \underset{x\rightarrow-1}{lim}\left(\sqrt{1+x^{2}}\right).

7) \underset{x\rightarrow0}{lim}\cfrac{x^{2}-2}{\sqrt{x+4}}.

8) \underset{x\rightarrow1}{lim}\cfrac{e^{x}-2x}{e^{x}-2}.

Pubblicato in Senza categoria | Lascia un commento