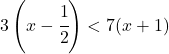Dato un insieme X ed un insieme Y la relazione tra un elemento di X ed un solo elemento di Y si chiama funzione.
Essa si indica con
![]()
L’insieme dei valori di X prende il nome di Dominio mentre i valori di Y prende il nome di codominio.
Esempi di funzione.
1- Per fare una frittata è indispensabile avere il fuoco, una padella, del sale, delle uova, allora potrò dire che
frittata=f(fuoco, padella, sale,uova) ossia è funzione del fuoco, della padella, del sale, delle uova ossia di quattro variabili.
Ad esempio il dominio del fuoco è la presenza dell’ossigeno e del carbonio, senza di questi due elementi il fuoco non esiste.
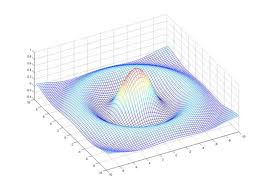
Studiare funzioni a più dimensioni è complesso e vengono rappresentate da grafici di questo tipo:
ossia della funzione:
![]()
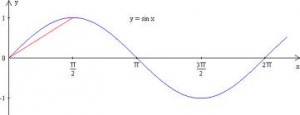
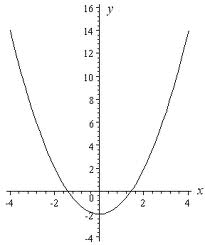
Ma per molti fenomeni è sufficiente usare un grafico a due dimensioni ossia studiare funzioni del tipo:
![]()
che hanno un grafico che rappresenta ad esempio il moto armonico ossia l’oscillazione di un pendolo, oppure l’andamento delle maree oppure la tensione elettrica ai capi di una resistenza in regime di corrente alternata.



![Rendered by QuickLaTeX.com \cfrac{1}{s^{3}}=L\left [ \cfrac{x^{2}}{2!} \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ecac936a25f0efc0abe8e54fd4199ef5_l3.png)
![Rendered by QuickLaTeX.com f(s)=\cfrac{e^{-5s}}{s^{3}}=L\left [\cfrac{(x-5)^{2}}{2!}\cdot H(x-5) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a93bf7df39c3f32c6370d33163c29130_l3.png)
![Rendered by QuickLaTeX.com f(s)=\cfrac{e^{-5s}}{(s-2)^{4}}=L\left [ \cfrac{\left ( t-5 right )^{3}}{6}e^{2(t-5)}cdot H(t-5) \right ]](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-95a144a76023a65211924855e3ccd6ef_l3.png)