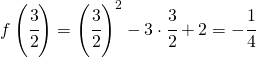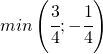Prima di affrontarle il mcm e MCD per i monomi è interessante richiamarli dal punto di vista algebrico:
m.c.m: il minimo comune multiplo è il prodotto di tutti i fattori comuni e non comuni presi con il massimo esponente.
M.C.D. il massimo comune divisore invece è il prodotto dei SOLI fattori comuni presi con l’esponente più basso.
Ecco una lezione interessante sul mcm tra monomi:
Ecco una lezione interessante sul M.C.D. tra i monomi
In matematica il concetto di infinito procura spesso grandi dubbi esattamente come la più grande poesia di ogni tempo che il genio di Leopardi ci ha regalato:
« Sempre caro mi fu quest’ermo colle,
e questa siepe, che da tanta parte
dell’ultimo orizzonte il guardo esclude.
Ma sedendo e mirando, interminati
spazi di là da quella, e sovrumani
silenzi, e profondissima quïete
io nel pensier mi fingo, ove per poco
il cor non si spaura. E come il vento
odo stormir tra queste piante, io quello
infinito silenzio a questa voce
vo comparando: e mi sovvien l’eterno,
e le morte stagioni, e la presente
e viva, e il suon di lei. Così tra questa
immensità s’annega il pensier mio:
e il naufragar m’è dolce in questo mare. »
Tornando però nell’ambito matematico l’infinito è un concetto collegato a quello di asintoto. L’asintoto è una retta immaginaria a cui la funzione cerca di avvicinarsi ma a cui non arriva mai.
E’ come il concetto di velocità della luce: ad essa non ci si può mai arrivare ma solo tendere in quanto per arrivarci bisognerebbe avere una massa infinitamente piccola se non nulla; tale velocità infatti è raggiungibile solo dall’energia!
Enrico Prampolini
Il concetto di limite è fondamentale per capire verso quale valore tende una funzione. In particolare mi interessa dettare delle regole pratiche per poterne fare un protocollo di attuazione immediata:
Ecco la sua forma più semplice ed immediata:
Come si legge?
Il limite per 
che tende a 
di 
vale 
.
Ho sostituito il valore a cui tende la nella funzione di partenza.
es.1
In questo caso il valore a cui tende la funzione coincide con il valore stesso della funzione in quel punto. Sembra una tautologia ma in realtà non è così: sia che ci si avvicini da destra che da sinistra a quel punto, il risultato non cambia.
Il concetto di limite destro e sinistro è fondamentale nello studio di funzione: a seconda che ci si avvicini da sinistra o da destra il valore della funzione potrebbe assumere dei valori diversi.
REGOLA PRATICA
Per sviluppare un limite la prima operazione è proprio quella di sostituire il valore a cui tende la alla funzione.
Fortunato Depero
3) Dato 
che appartengono al primo quadrante e che:
Dimostrare che:
Sviluppo
(1) 
ossia
(2) 
Adesso utilizzo la (1)
![tanalpha=cfrac{sinalpha}{cosalpha}=cfrac{sinleft(cfrac[l]{pi}{4}-betaright)}{cosleft(cfrac{pi}{4}-betaright)}=cfrac{sincfrac{pi}{4}cosbeta-sinbetacoscfrac{pi}{4}}{coscfrac{pi}{4}cosbeta+sincfrac{pi}{4}sinbeta}=cfrac{1}{2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a10f0ac6db51364ed3da397a95eb06ba_l3.png "Rendered by QuickLaTeX.com")
quindi utilizzando anche la (2) e sviluppando il seno di 45° ed il coseno di 45° ho:
Gino Severini
2) Dato un triangolo i cui angoli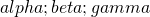 
seguono le seguenti relazioni:
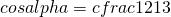
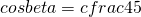
dire se tale triangolo è acutangolo o ottusangolo e determinare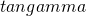 
.
Sviluppo
Un triangolo si dice acutangolo quando ha tutti e tre gli angoli minori di 90°.
Un triangolo si dice ottusangolo quando un angolo è ottuso ossia maggiore di 90°.
Nel caso specifico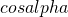 
è positivo per cui 
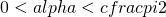non potrà mai essere tra 
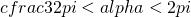perchè la somma degli angoli interni di un triangolo è sempre 180°.
Lo stesso ragionamento vale per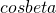 
.
Quindi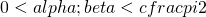 
e non si può ancora dire se il terzo angolo sia maggiore o minore di 90° condizione che ci fa affermare se avere un acutangolo o un ottusangolo.
Allora, sempre per la relazione fondamentale che la somma degli angoli interni di un triangolo è 180°,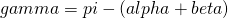 
.
(1) ![tanleft[pi-(alpha+beta)right]=-tanleft(alpha+betaright)=cfrac{sinalphacosbeta+sinbetacosalpha}{sinalphasinbeta-cosalphacosbeta}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-28e03625f02c7a9044389068955e0998_l3.png "Rendered by QuickLaTeX.com")
Adesso ho:
(2) 
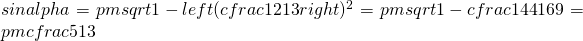
prendo il valore positivo in quanto .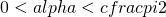
(3) 
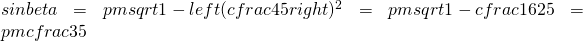
prendo il valore positivo in quanto 
.
Adesso sostituisco i valori dati dal problema e la (2) e la (3) nella (1) e risulta:
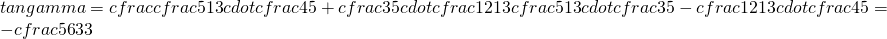
La tangente assume un valore negativo tra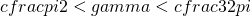 
per cui alla fine mi troverò un ottusangolo!
Fortunato Depero
1) Dato un triangolo i cui angoli () seguono le seguenti relazioni:
con 
con
Determinare il 
.
Sviluppo:
ossia
devo determinare:
(1) ![singamma=sinleft[pi-(alpha+beta)right]=sin(alpha+beta)=sinalphacosbeta+cosalphasinbeta](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-679f2f2b9e59ac751845718361ba68d7_l3.png "Rendered by QuickLaTeX.com")
in cui ho utilizzato le formule di addizione.
siccome in trigonometria vale la relazione fondamentale che è la diretta conseguenza del teorema di Piragora:
allora
devo prendere il segno positivo o negativo?
Siccome il 
è positivo per allora prendo il segno positivo ed ho quindi:
(2) 
In maniera analoga ho:
Prendo il segno positivo perchè 
è positivo per
quindi:
(3) 
Adesso sostituisco la (2) e la (3) nella (1) prendendo anche i dati di partenza e risulta:
razionalizzando (ossia moltiplicando per 
sia il numeratore che il denominatore) il risultato conclusivo diventa:
Il triangolo di Tartaglia rimane una pietra miliare che indica il passaggio dai più conosciuti prodotti notevoli a quelli meno usati.
Tale post è stato richiesto da un alunno (A.M.O.) che si chiedeva perchè non si potessero avere i prodotti successivi!
Propedeutico è esplicitare tutti gli esponenti dei binomi per apprezzare compeltamente la schematizzazione.
adesso se si vuole scrivere l’elevamento a potenza successivo è indispensabile avere il triangolo di Tartaglia:
_______
–> 
______
–>
_____
–>
____
–>
___
–>
quindi la quarta riga mi fornisce:
Come si crea il triangolo di Tartaglia?
Ad esempio nella quinta riga il 5 è dato dalla somma dell’1 e del 4 della riga precedente.
Il 10 è dato dalla somma del 4 e del 6 della riga precedente e così via.
Rene Magritte - Il mistero della natura
Osservando il grafico presente nel post precedente si possono evincere gli angoli fondamentali:
Attenzione però alla seguente notazione:
In trigonometria si utilizza sempre tale notazione per indicare il valore degli angoli.
DA IMPARARE
In maniera analoga le seguenti:
Le formule di addizione permettono lo svolgimento di molti problemi; eccole!
Dalla circonferenza goniometrica e dalle formule precedenti posso trovare le seguenti relazioni:
La trigonometria mette in relazione il valore degli angoli di un triangolo rettangolo con i lati.
Le sue applicazioni si possono trovare in astronomia, in fisica, in geologia ed anche nella musica.
Tolomeo è stato il primo a trattare la materia in maniera formale applicandola allo studio teorico della geometria e di tutti i poligoni inscritti in una circonferenza.
Data la seguente figura:
Le relazione che lega il valore dell’angolo al lato è la seguente:
un’ulteriore funzione è la seguente:
A questo punto per meglio immaginare cosa sono il seno ed il coseno è corretto rappresentarli sul piano cartesiano
y=tan(x)$
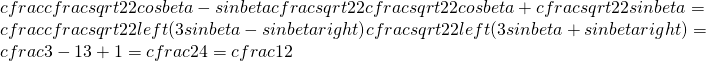
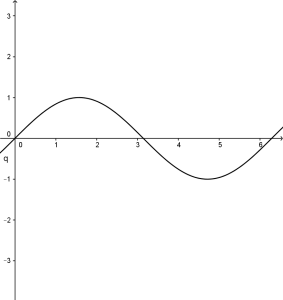
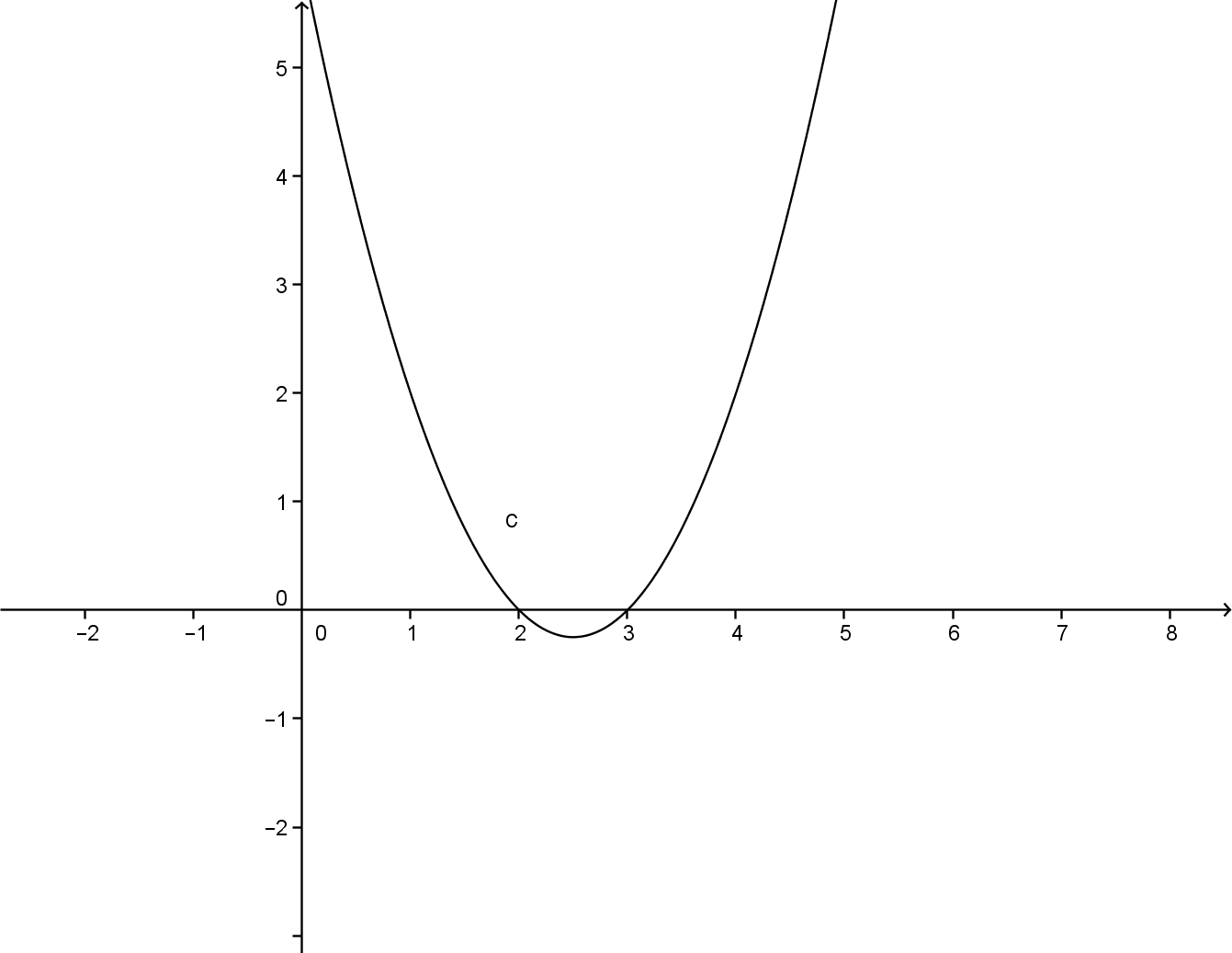
Una volta che si riesce a calcolare la derivata prima di una funzione si può cominciare ad intuire come potrà essere il suo grafico. In particolare siccome la derivata prima fornisce il valore dell’inclinazione della curva tangente si può capire che quando essa si annulla la relativa retta è orizzontale.
A questo punto posso, studiando il segno della derivata prima capire quando cresce e quando decresce la funzione.
Partendo dall’esempio più banale che possa esserci cerco di chiarire il concetto.
Sia 
.
Calcolo la derivata prima:
Il punto in cui si annulla si ottiene annullando la derivata prima:
ossia
Esso è un punto di massimo o minimo?
Risolvo la disequazione
Essa è positiva per
E’ facilmente dimostrabile che quando la derivata prima è negativa la funzione è decrescente e quando la derivata prima è positiva è crescente.
Per cui la mia funzione di partenza (parabola) è:
è il punto di minimo (in questo caso anche assoluto della funzione).Per trovare il valore della relativa ordinata del punto di minimo si sostituisce alla funzione di partenza il valore trovato:
Ossia il punto di minimo ha coordinate:
Il grafico della funzione è:
