(1) ![Rendered by QuickLaTeX.com \cfrac{\left(\cfrac{3}{4}-0,0\overline{3}\right)\cdot\cfrac{3}{43}+\left(2,\overline{4}-1,2\right)\cdot\cfrac{9}{7}-\cfrac{8}{5}}{\left[\cfrac{2,3-2,\overline{15}}{0,2+1,\overline{3}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(1+\cfrac{1}{4}\right)}+\cfrac{4}{0,\overline{2}+1,2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-02d65e94d0917de7b9476a0094a75a18_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{3}{90}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{24-2}{9}-\cfrac[l]{12}{10}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{215-2}{99}}{\cfrac{2}{10}+\cfrac{13-1}{9}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(\cfrac{5}{4}\right)}+\cfrac{4}{\cfrac{2}{9}+\cfrac{12}{10}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-28424d303d5ce665cd63a30d935d0762_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{1}{30}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{22}{9}-\cfrac[l]{6}{5}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{213}{99}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{20+108}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-06555bd3c875b67329729bd153b46c89_l3.png)
passaggio successivo
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{45-2}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{110-54}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{71}{33}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{128}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3ec27b70796301863401cdf0ea8bf38_l3.png)
e quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{43}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{56}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{759-710}{330}}{\cfrac{9+60}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+4\cdot\cfrac{90}{128}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9bb9ead11586bffd4188482c94e631_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}+\cfrac{8}{5}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{49}{330}}{\cfrac{69}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8e9af0d21b6955edb5cbb40dca7c8a6b_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{49}{330}\cdot\cfrac{45}{69}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79d070175d19f76c39957311f4a0d823_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{1}{2}+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4df53411cdfe99cd68512672fe340b24_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{5}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ab6f29207a5418baa8c16b081937aeea_l3.png)
e
![]()
ed infine
![]()
(2) ![Rendered by QuickLaTeX.com \cfrac{\left[\left(2+\cfrac{1}{2}\right)^{2}\cdot\left(3-\cfrac{4}{3}\right)^{2}\cdot\left(-1-\cfrac{1}{5}\right)^{2}\right]^{-1}:\left(-1+\cfrac{4}{5}\right)^{2}}{\cfrac{1}{2}\cdot\left(-\cfrac{1}{3}\right)^{-2}+\left(\cfrac{1}{4}\right)^{2}\cdot\left(1-\cfrac{3}{8}\right)^{-2}:\left(1-\cfrac{3}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3622f616b5ce34a9e5c15ffa6f238d29_l3.png)
Risultato ![]()
![Rendered by QuickLaTeX.com \cfrac{\left[\left(\cfrac{5}{2}\right)^{2}\cdot\left(\cfrac{5}{3}\right)^{2}\cdot\left(-\cfrac{6}{5}\right)^{2}\right]^{-1}:\left(-\cfrac{1}{5}\right)^{2}}{\cfrac{1}{2}\cdot9+\cfrac{1}{4^{2}}\cdot\left(\cfrac{5}{8}\right)^{-2}:\left(\cfrac{2}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a6b6425e1de27a0a44f4b98eef018394_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac{\left[\cfrac{5^{2}}{2^{2}}\cdot\cfrac{5^{2}}{3^{2}}\cdot\cfrac{6^{2}}{5^{2}}\right]^{-1}\cdot5^{2}}{\cfrac{9}{2}+\cfrac{1}{4^{2}}\cdot\cfrac{8^{2}}{5^{2}}\cdot\cfrac{5^{2}}{2^{2}}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d384a8e0549ec3dc52748f4931cbb4cf_l3.png)
ed infine
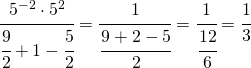
Come conclusione
[paypal-donation]
(1) ![Rendered by QuickLaTeX.com \cfrac{\left(\cfrac{3}{4}-0,0\overline{3}\right)\cdot\cfrac{3}{43}+\left(2,\overline{4}-1,2\right)\cdot\cfrac{9}{7}-\cfrac{8}{5}}{\left[\cfrac{2,3-2,\overline{15}}{0,2+1,\overline{3}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(1+\cfrac{1}{4}\right)}+\cfrac{4}{0,\overline{2}+1,2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-02d65e94d0917de7b9476a0094a75a18_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{3}{90}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{24-2}{9}-\cfrac[l]{12}{10}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{215-2}{99}}{\cfrac{2}{10}+\cfrac{13-1}{9}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(\cfrac{5}{4}\right)}+\cfrac{4}{\cfrac{2}{9}+\cfrac{12}{10}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-28424d303d5ce665cd63a30d935d0762_l3.png)
quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{3}{4}-\cfrac{1}{30}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{22}{9}-\cfrac[l]{6}{5}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{213}{99}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{20+108}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-06555bd3c875b67329729bd153b46c89_l3.png)
passaggio successivo
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{45-2}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{110-54}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{23}{10}-\cfrac{71}{33}}{\cfrac{1}{5}+\cfrac{12}{9}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{4}{\cfrac{128}{90}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-e3ec27b70796301863401cdf0ea8bf38_l3.png)
e quindi
![Rendered by QuickLaTeX.com \cfrac[l]{\left(\cfrac{43}{60}\right)\cdot\cfrac{3}{43}+\left(\cfrac[l]{56}{45}\right)\cdot\cfrac{9}{7}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{759-710}{330}}{\cfrac{9+60}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+4\cdot\cfrac{90}{128}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-9f9bb9ead11586bffd4188482c94e631_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}+\cfrac{8}{5}-\cfrac[l]{8}{5}}{\left[\cfrac{\cfrac{49}{330}}{\cfrac{69}{45}}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-8e9af0d21b6955edb5cbb40dca7c8a6b_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{49}{330}\cdot\cfrac{45}{69}\cdot\left(\cfrac{253}{49}\right)+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-79d070175d19f76c39957311f4a0d823_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{1}{2}+\cfrac{3}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-4df53411cdfe99cd68512672fe340b24_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac[l]{\cfrac{1}{20}}{\left[\cfrac{5}{4}\right]\cdot\left(\cfrac{4}{5}\right)}+\cfrac{90}{32}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-ab6f29207a5418baa8c16b081937aeea_l3.png)
e
![]()
ed infine
![]()
(2) ![Rendered by QuickLaTeX.com \cfrac{\left[\left(2+\cfrac{1}{2}\right)^{2}\cdot\left(3-\cfrac{4}{3}\right)^{2}\cdot\left(-1-\cfrac{1}{5}\right)^{2}\right]^{-1}:\left(-1+\cfrac{4}{5}\right)^{2}}{\cfrac{1}{2}\cdot\left(-\cfrac{1}{3}\right)^{-2}+\left(\cfrac{1}{4}\right)^{2}\cdot\left(1-\cfrac{3}{8}\right)^{-2}:\left(1-\cfrac{3}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3622f616b5ce34a9e5c15ffa6f238d29_l3.png)
Risultato ![]()
![Rendered by QuickLaTeX.com \cfrac{\left[\left(\cfrac{5}{2}\right)^{2}\cdot\left(\cfrac{5}{3}\right)^{2}\cdot\left(-\cfrac{6}{5}\right)^{2}\right]^{-1}:\left(-\cfrac{1}{5}\right)^{2}}{\cfrac{1}{2}\cdot9+\cfrac{1}{4^{2}}\cdot\left(\cfrac{5}{8}\right)^{-2}:\left(\cfrac{2}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-a6b6425e1de27a0a44f4b98eef018394_l3.png)
e
![Rendered by QuickLaTeX.com \cfrac{\left[\cfrac{5^{2}}{2^{2}}\cdot\cfrac{5^{2}}{3^{2}}\cdot\cfrac{6^{2}}{5^{2}}\right]^{-1}\cdot5^{2}}{\cfrac{9}{2}+\cfrac{1}{4^{2}}\cdot\cfrac{8^{2}}{5^{2}}\cdot\cfrac{5^{2}}{2^{2}}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-d384a8e0549ec3dc52748f4931cbb4cf_l3.png)
ed infine
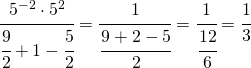
Come conclusione
[paypal-donation]La formula di sdoppiamento viene utilizzata per:
DETERMINARE LA RETTA TANGENTE AD UN’ELLISSE IN UN PUNTO CHE APPARTIENE ALL’ELLISSE STESSA
Eccola:
![]()
L’equazione dell’ellisse è:
(1) ![]()
il punto ![]() appartiene all’ellisse per cui è soddisfatta la seguente identità:
appartiene all’ellisse per cui è soddisfatta la seguente identità:
(2) ![]()
Sottraggo la (2) alla (1) e risulta:
(3) ![]()
semplifico e sviluppo i due binomi tra parentesi come la differenza di binomi:
(4) ![]()
Considerando adesso che l’equazione della retta passante per il punto P ha equazione:
(5) ![]()
sostituisco la (5) nella (4), quest’ultima diventa:
(6) ![]()
posso dividere il tutto per ![]()
e la (6) diventa:
(7) ![]()
siccome il punto P appartiene a questa curva sostituendo le sue coordinate la (7) diventa:
(8) ![]()
sviluppando i monomi si ha:
(9) ![]()
Risolvendola rispetto all’incognita m ho:
(10) ![]()
Sostituendo adesso la (10) nell’equazione generica della retta (5) si ha:
(11) ![]()
(12) ![]()
(13) ![]() ordinandola
ordinandola
(14) ![]() e sapendo dalla (3) che:
e sapendo dalla (3) che:
(15) ![]()
sostuendo la (15) nella (14) si ha:
(16) ![]()
adesso dividendo entrambi membri per ![]()
ho proprio la formula che cercavo ossia:
(17) ![]()
(1.a) ![]()
(1.b) ![]()
(1.c) ![]()
(1.d) ![]()
(1.e) ![]()
(1.f) ![]()
(1.g) ![]()
(2.a) ![]()
(2.b) ![]()
(2.c) ![]()
(2.d) ![]()
(2.e) ![]()
(2.f) ![]()
(3.a) 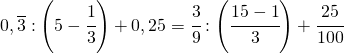
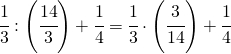
![]()
(3.b) 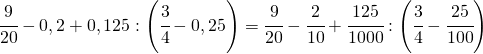
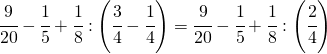
![]()
![]()
(3.c) 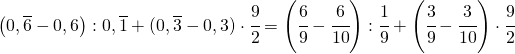
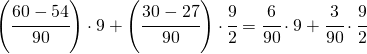
![]()
(4) Leggendo il testo si nota che tutti i dati si riferiscono a promossi a prescindere che questi lo siano stati a giugno (“per merito”) o a settembre(“debito formativo”). Sommo le rispettive percentuai e trovo che ![]() ossia la totalità è stata promossa. I respinti quindi non ve ne saranno.
ossia la totalità è stata promossa. I respinti quindi non ve ne saranno.
(5) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(6) Il perimetro è datto da ![]()
(7) Area del triangolo isocele ![]() sostituendo i valori dati ho:
sostituendo i valori dati ho: ![]()
Per determinare il perimetro devo trovare il valore dei lati obliqui ossia applicare il teorema di pitagora conoscendo la lunghezza dei due cateti che sono entrambi 5. Infatti metà della base lunga 10 fa proprio 5.
![]()
Il perimetro sarà quindi:
![]()
(8) Si ha un trapezio scaleno ossia con tutti e quattro i lati diversi. Il perimetro è la somma dei quattro lati:
![]()
Alla base delle attuali conoscenza non si riesce a calcolare l’altezza per cui per calcolare l’area manca il dato sull’altezza.
(9) Partendo dalla domanda.
Si calcoli il valore delle seguenti espressioni:
(1) ![Rendered by QuickLaTeX.com \cfrac{\left(\cfrac{3}{4}-0,0\overline{3}\right)\cdot\cfrac{3}{43}+\left(2,\overline{4}-1,2\right)\cdot\cfrac{9}{7}-\cfrac{8}{5}}{\left[\cfrac{2,3-2,\overline{15}}{0,2+1,\overline{3}}\cdot\left(5+\cfrac{8}{49}\right)+\cfrac{3}{4}\right]:\left(1+\cfrac{1}{4}\right)}+\cfrac{4}{0,\overline{2}+1,2}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-02d65e94d0917de7b9476a0094a75a18_l3.png) Risultato
Risultato ![]()
(2) ![Rendered by QuickLaTeX.com \cfrac{\left[\left(2+\cfrac{1}{2}\right)^{2}\cdot\left(3-\cfrac{4}{3}\right)^{2}\cdot\left(-1-\cfrac{1}{5}\right)^{2}\right]^{-1}:\left(-1+\cfrac{4}{5}\right)^{2}}{\cfrac{1}{2}\cdot\left(-\cfrac{1}{3}\right)^{-2}+\left(\cfrac{1}{4}\right)^{2}\cdot\left(1-\cfrac{3}{8}\right)^{-2}:\left(1-\cfrac{3}{5}\right)^{2}-\cfrac{5}{2}}](https://www.whymatematica.com/wp-content/ql-cache/quicklatex.com-3622f616b5ce34a9e5c15ffa6f238d29_l3.png) Risultato
Risultato ![]()
Risolvi i seguenti problemi
(3) La differenza tra la base e l’altezza di un triangolo è di 26,6 cm. Sapendo che l’altezza è i ![]() della base, determinare l’area del triangolo.
della base, determinare l’area del triangolo.
(4) Un ragazzo riesce a montare un computer in 6 ore, mentre un suo amico ne impiega 3. In quanto tempo riescono ad assemblare 5 computer, lavorando assiene?
(5) Due amici abitano su uno stesso viale, ma da parti opposte. Dopo essersi chiamati con il cellualre, escono da casa per incontrarsi. Trascorso un certo tempo, il primo ragazzo ha percorso i ![]() della strada e il secondo i
della strada e il secondo i ![]() e la loro distanza è di 600m. Quanto è lungo il viale?
e la loro distanza è di 600m. Quanto è lungo il viale?
(6) Ordina in senso crescente i seguenti sei numeri razionali, poi scrivi il quarto numero.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
(7) Cosa si intende per notazione scientifica e fai dieci esempi di un suo utilizzo.
(8) Perchè sono utili le frazioni?
La formula di sdoppiamento viene utilizzata per
DETERMINARE LA RETTA TANGENTE ALLA CIRCONFERENZA IN UN PUNTO CHE APPARTIENE ALLA CIRCONFERENZA
Eccola:
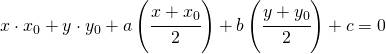
DIMOSTRAZIONE
L’equazione della circonferenza è:
(1) ![]()
il punto ![]() appartiene alla circonferenza per cui è soddisfatta la seguente identità:
appartiene alla circonferenza per cui è soddisfatta la seguente identità:
(2) ![]()
Sottraggo la seconda alla prima e si ha:
(3) ![]()
semplifico, sviluppo i due binomi tra parentesi come la differenza di binomi e raggruppo diventa:
(4) ![]()
Considerando adesso che l’equazione della retta passante per il punto P ha equazione:
(5) ![]()
sostituisco la (5) nella (4), quest’ultima diventa:
(6) ![]()
posso dividere il tutto per ![]()
e la (6) diventa:
(7) ![]()
siccome il punto P appartiene a questa curva sostituendo le sue coordinate la (7) diventa:
(8) ![]() sviluppando le parentesi
sviluppando le parentesi
(9) ![]() sommando i monomi uguali ho:
sommando i monomi uguali ho:
(10) ![]() risolvendola rispetto la variabile m:
risolvendola rispetto la variabile m:
(11) ![]() .
.
Ultimo passo è sostituire la (11) nell’equazione generica della retta (5) che diventa:
(12) ![]()
facendo il m.c.m. ho:
(13) ![]() ) sviluppando il prodotto dei binomi e portando tutto dalla stessa parte:
) sviluppando il prodotto dei binomi e portando tutto dalla stessa parte:
(14) ![]() riordinando i vari termini ho
riordinando i vari termini ho
(15) ![]()
ora dalla (2) so che:
(16) ![]() sostituendola al binomio tra parentesi e sviluppando la moltiplicazione per 2 ho:
sostituendola al binomio tra parentesi e sviluppando la moltiplicazione per 2 ho:
(17) ![]() e sommando i binomi risulta:
e sommando i binomi risulta:
(18) ![]() dividendo per 2 tutti i monomi risulta la formula di sdoppiamento conosciuta:
dividendo per 2 tutti i monomi risulta la formula di sdoppiamento conosciuta:
(19) 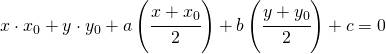
[:it]

Samy Charnine
6.1) ![]()
6.2) ![]()
6.3) ![]()
6.4) ![]()
6.5) ![]()
6.6) ![]()
6.7) ![]()
6.8) ![]()
6.9) ![]()
6.10) ![]()
Soluzioni a tutti gli esercizi precedenti[:en]1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]() [:de]1)
[:de]1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]() [:]
[:]
Il programma che segue applica il teorema di Ruffini.
Si evidenziano le seguenti cose:
– la prima parte chiede soltanto i coefficienti del polinomio da quellocon grado più elevato fino al termine noto–> salva i dati in una lista di nome polinomio
– la seconda parte determina i divisori del termine noto salvandoli in una lista di nome divisori.
– la terza parte verifica quali tra i divisori sono gli zeri del polinomio
Quest’ultima parte è la più complessa in quanto vi sono due cicli for uno dentro all’altro.
Per capirlo nei dettagli bisogna togliere il cancelletto nella parte commentata per seguire nei passi il ragionamento.
E’ la parte più complicata oggettivamente per programmatori esperti.
Le soluzioni trovate le salvo ancora in una lista e controllo il numero di elementi per emettere il messaggio corretto.
Notare quanto sia importante la fase dichiarativo
Ma ecco il programma:
################################
# Teorema di ruffini
# autore Francesco Bragadin
################################
#Area dichiarativa
polinomio=[]
divisori=[]
soluzioni=[]
sommafinale=0
divisore=1
###########################
#parte prima
#inserimento coefficienti
###########################
print “Programma teorema di Ruffini”
entrata = raw_input(“Inserisci un coefficiente? [y/n]”)
while entrata==”y”:
p=input(“coefficiente: “)
polinomio.append(p)
entrata= raw_input(“Inserisci un coefficiente? [y/n]”)
print “ecco il mio polinomio”
print polinomio
#######################################
#parte seconda
# scoperta divisori del termine noto
#######################################
#lunghezza polinomio
# o meglio quanti elementi contiene?
elementipolinomio = len(polinomio)
#il termine noto è l’ultimo elemento della lista
# il primo elemento è quello con indice zero mentre
# l’ultimo è quello identificato da ep-1
terminenoto = polinomio[elementipolinomio-1]
print “Il termine noto è: “,terminenoto
if terminenoto<0:
terminenoto=-terminenoto
#continuo il ciclo finchè il divisore non è uguale ad termine noto
while divisore<=terminenoto:
resto=terminenoto%divisore
if resto==0:
divisori.append(divisore)
#se è un divisore devo prendere anche il suo opposto
divisori.append(-divisore)
# incremento il divisore sempre di uno
divisore=divisore+1
print “Ecco i divisori!”
print divisori
############################################
# parte terza
# quali sono gli zeri del polinomio?
############################################
#quanti sono i divisori?
numerodivisori=len(divisori)
for i in range(numerodivisori):
for j in range(elementipolinomio):
###############################################################################
# serve per controllare il ciclo
# print polinomio[j],” “,divisori[i],” “,(elementipolinomio-1-j)
###############################################################################
sommaparziale=polinomio[j]*(divisori[i]**(elementipolinomio-1-j))
sommafinale=sommafinale+sommaparziale
###############################################################################
# serve per controllare il ciclo
# print sommafinale
###############################################################################
if sommafinale==0:
# metto gli zeri in una lista
soluzioni.append(divisori[i])
# devo ripartire dal primo elemento del polinomio
# devo rimettere a zeo la sommafinale
j=0
sommafinale=0
numerosoluzioni=len(soluzioni)
if numerosoluzioni==0:
print “Non ci sono soluzioni”
if numerosoluzioni==1:
print “la soluzione è: “,soluzioni[0]
if numerosoluzioni >1:
print “le soluzioni sono:”
print soluzioni
Le equazioni di secondo grado spurie non hanno la necessità di essere risolte utilizzando la formula risolutiva.
Nel caso specifico esse hanno sempre la c = 0.
Una delle due soluzioni è sempre ![]() (ZERO).
(ZERO).
Ecco il metodo risolutivo valido sempre.
![]()
![]()
Una soluzione è
![]()
e l’altra risolve l’equazione di primo grado
![]() ossia
ossia ![]()
Ecco alcuni esericizi che possono aiutare a prendere confidenza sulle spurie.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
Le equazioni di secondo grado pure hanno la caratteristica fondamentale che le due soluzioni sono opposte.
In particolare la b è nulla.
Non conviene applicare la formula risolutiva ma usare soltanto il seguente metodo. Utilizzo un esempio, sperando di essere più chiaro.
![]()
Si risolve nella seguente maniera:
![]()
risolvendo abbiamo
![]()
Ecco alcuni esercizi che possono aiuatare ad allenarci alla soluzione:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
In quest’ultimo caso cosa succede?
1) dati i seguenti numeri decimali (limitati e periodici) trovare la relativa frazione generatrice:
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. ![]()
e. ![]()
2) Scrivere le seguenti frazioni sotto forma di numero decimale, precisando di che numero decimale si tratta (limitato o periodico).
a. ![]()
b. ![]()
e. ![]()
f. ![]()
g. ![]()
h. ![]()
3. Calcolare il valore delle seguenti espressioni
a. 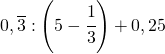
b. 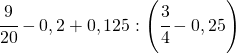
c. ![]()
4. Alla fine dell’anno scolastico i risultati di una classe di 28 alunni sono i seguenti:
Quanti sono gli alunni respinti?
5. Sviluppare le seguenti equivalenze utilizzando facoltativamente la notazione scientifica:
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. ![]()
g. ![]()
h. ![]()
6. Dato un rettangolo con dimensioni 5 e 6 calcolarne il perimetro
7. Dato un triangolo isoscele di cui si conosce la base e l’altezza (rispettivamente 10cm e 5cm ), calcolarne l’area e facoltativamente il perimetro
8. Dato un trapezio con base maggiore di 6cm, base minore 3cm ed il primo lato obliquo 3,4cm ed il secondo 3,04cm. Calcolare il perimetro e l’area.
9. Sapendo che per recintare un appezzamento di terreno di forma quadrata ho utilizzato 121m di corda. Quante zolle di terra dovrò utilizzare considerando il fatto che ogni zolla ha le seguenti dimensioni: 20cmx30cm?